题目内容
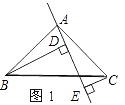
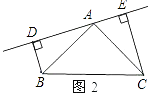
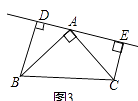
【题目】一组连续奇数按如图方式排列,请你解决下列问题:
(1)第7行最后一个数字是 , 在第15行第4列的数字是;
(2)请用n的代数式表示第n行的第1个数字和最后一个数字;
(3)现用一个正方形框去围出相邻两行中的4个数字
(例如:第4行和第5行的15,17,23,25),
请问能否在第50行和第51行中 围出4个数字的和是10016?若能,请求出这4个数字;若不能,请说明理由.
【答案】
(1)55,217
(2)解:第n行的第1个数字为:n-n+1,
最后一个数字为n+n-1;
(3)解:能.因为第50行的第一个数为502-50+1=2451
则第50行第k个数为2451+2k、第k+1个数为2451+2(k+1),
第51行第k个数为2551+2k、第k+1个数为2551+2(k+1),
2451+2k+2451+2(k+1)+2551+2k+2551+2(k+1)=10016,
解得,10008+4k=10016,k=2,
所以这四个数分别为:2453,2455,2553,2555.
【解析】解:(1)∵第六行的最后一个数字为41,
∴第7行最后一个数字为41×2+7=55;
∵第15行第一个数字为1+(1+2+3+……+14)×2=211,
∴第15行第4个数字为211+2×3=217.
(1)根据第六行的最后一个数字,将其+2×7可得第一个空;第15行第一个数字为1+(1+2+3+……+14)×2,将其+2×3可得第二个空;
(2)由所给的数列可得第n行第1个数字,再由第n行最后一个数字为第(n+1)行第一个数字-2可得答案;
(3)根据(2)中得出的结论可求得第50、51行第一个数字,进而可得第50、51行第k、k+1列的四个数字,然后得到关于k的方程,从而解出k的值,进而得到答案.