Question

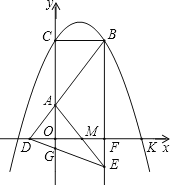
【题目】如图，y=﹣x2+mx+3（m＞0）与y轴交于点C，与x指的正半轴交于点k，过点C作CB∥x轴交抛物线于另一点B，点D在x轴的负半轴上，连结BD交y轴于点A，若AB=2AD．

（1）用含m的代数式表示BC的长；

（2）当m=2时，判断点D是否落在抛物线上，并说明理由；

（3）过点B作BE∥y轴交x轴于点F，延长BF那至E，使得EF=BC，连结DE交y轴于点G，连结AE交x轴于点M，若△DOG的面积与△MFE的面积之比为1：2，则求出抛物线的解析式．

Answer 1

【答案】（1）BC=m；（2）当m=2时，点D落在抛物线上；（3）y=﹣x2+x+3．

【解析】

（1）因为抛物线的对称轴为x＝，由对称性即可得出BC的长；

（2）当m＝2时，BC＝2，由题意，可得△AOD∽△ACB，利用相似三角形对应边成比例求得点D（﹣1，0），即可判断点D是否落在抛物线上；

（3）由△AOD∽△ACB，求得A（0，1），D（﹣，0），因为点E（m，﹣），用待定系数法分别求得直线AE，DE的表达式，即可得出点M，点G的坐标，根据△DOG的面积与△MFE的面积之比为1：2，列出方程，解方程即可求得m的值．

（1）∵y=﹣x2+mx+3（m＞0）．

∵抛物线的对称轴为x=，

∴BC=m．

（2）当m=2时，BC=2，y=﹣x2+2x+3

∵CB∥x轴，

∴△AOD∽△ACB，

∴DO：BC=AD：AB=1：2，

∴DO=1，即点D（﹣1，0），

当x=﹣1时，y=﹣（﹣1）2+2×（﹣1）+3=0，

∴当m=2时，点D落在抛物线上；

（3）∵过点B作BE∥y轴交x轴于点F，延长BF至E，使得EF=BC，

∴点E（m，﹣）．

∵C（0，3），OD：BC=OA：AC=AD：AB=1：2，

∴OA=1，OD=，

∴A（0，1），D（﹣，0），

设直线AE表达式为y=kx+b，把E（m，﹣），A（0，1）代入得

∴，

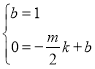解得：，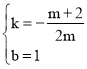

∴直线AE表达式为y=﹣x+1，

∴点M坐标为（，0），

设直线DE表达式为y=ax+t，

将D（﹣，0），E（m，﹣）代入得，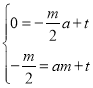

解得：，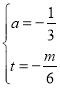

∴直线DE表达式为y=﹣x﹣，

∴点G坐标为（0，﹣）．

∵△DOG的面积与△MFE的面积之比为1：2，

∴2×××=××（m﹣）．

∵m＞0，∴m=1．

故该抛物线解析式是：y=﹣x2+x+3．