题目内容
【题目】为建设天府新区“公园城市”,实现城市生活垃圾减量化、资源化、无害化的目标.近日,成都市天府新区计划在各社区试点实施生活垃圾分类处理活动,取得市民积极响应.某创业公司发现这一商机,研发生产了一种新型家庭垃圾分类桶,并投入市场试营销售.已知该新型垃圾桶成本为每个40元,市场调查发现,该垃圾桶每件售价y(元)与每天的销售量为x(个)的关系如图.为推广新产品及考虑每件利润因素,公司计划每天的销售量不低于1000件且不高于2000件.
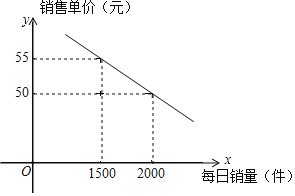
(1)求每件销售单价y(元)与每天的销售量为x(个)的函数关系式;
(2)设该公司日销售利润为W(元),求每天的最大销售利润是多少元?
【答案】(1)y=﹣0.01x+70;(2)最大销售利润是22500元
【解析】
(1)设y与x的函数解析式为:y=kx+b(k≠0),将函数图象上的两个点的坐标代入列出方程组,进行解答便可;
(2)根据“利润=(售价﹣进价)×销售量“列出函数解析式,然后根据二次函数的性质,求出其最大值.
解:(1)设y与x的函数解析式为:y=kx+b(k≠0),
∵函数图象过点(1500,55)和(2000,50),
∴![]() ,
,
∴![]() ,
,
∴y与x的函数解析式为:y=﹣0.01x+70;
(2)由题意得,
w=(y﹣40)x=(﹣0.01x+70﹣40)x=﹣0.01x2+30x,
即w=﹣0.01x2+30x,
∵﹣0.01<0,
∴当x=![]() 时,
时,
![]() ,
,
∵1000≤x≤2000,
∴当每天销售1500件时,利润最大为22500元.
∴每天的最大销售利润是22500元.

练习册系列答案
相关题目