题目内容
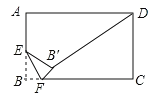
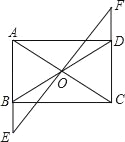
【题目】如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB、CD的延长线分别交于E、F.
(1)证明:△BOE≌△DOF;
(2)当EF⊥AC时,求证四边形AECF是菱形.
【答案】(1)(2)证明见解析
【解析】
(1)根据矩形的性质,通过“角角边”证明三角形全等即可;
(2)根据题意和(1)可得AC与EF互相垂直平分,所以四边形AECF是菱形.
(1)证明:∵四边形ABCD是矩形,
∴OB=OD,AE∥CF,
∴∠E=∠F(两直线平行,内错角相等),
在△BOE与△DOF中,
 ,
,
∴△BOE≌△DOF(AAS).
(2)证明:∵四边形ABCD是矩形,
∴OA=OC,
又∵由(1)△BOE≌△DOF得,OE=OF,
∴四边形AECF是平行四边形,
又∵EF⊥AC,
∴四边形AECF是菱形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目