题目内容
【题目】如图,△ABC在平面直角坐标系中,A(﹣2,5),B(﹣3,2),C(﹣1,1).
(1)请画出△ABC关于y轴的对称图形△A′B′C′,其中A点的对应点是A′,B点的对应点是B′,C点的对应点是C′,并写出A′,B′,C′三点的坐标.
(2)求△A′B′C′的面积.
【答案】(1)如图所示,△A′B′C′即为所求,见解析;A'(2,5),B'(3,2),C'(1,1);(2)△A′B′C′的面积为3.5.
【解析】
(1)依据轴对称的性质,即可画出△ABC关于y轴的对称图形△A′B′C′,即可得到A′,B′,C′三点的坐标.
(2)依据割补法即可得到△A′B′C′的面积.
(1)如图所示,△A′B′C′即为所求,A'(2,5),B'(3,2),C'(1,1).
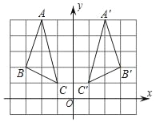
(2)△A′B′C′的面积为:2×4﹣![]() ×1×2﹣
×1×2﹣![]() ×1×3﹣
×1×3﹣![]() ×1×4=8﹣1﹣1.5﹣2=3.5.
×1×4=8﹣1﹣1.5﹣2=3.5.

练习册系列答案
相关题目
【题目】新春佳节来临,某公司组织10辆汽车装运苹果、芦柑、香梨三种水果共60吨去外地销售,要求10辆汽车全部装满,每辆汽车只能装运同一种水果,且装运每种水果的车辆都不少于2辆,根据下表提供的信息,解答以下问题:
苹果 | 芦柑 | 香梨 | |
每辆汽车载货量 | 7 | 6 | 5 |
每车水果获利 | 2500 | 3000 | 2000 |
![]() 设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围
设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围
![]() 用w来表示销售获得的利润,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值.
用w来表示销售获得的利润,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值.