题目内容
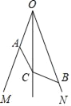
【题目】如图,OC平分∠MON,A、B分别为OM、ON上的点,且BO>AO,AC=BC,求证:∠OAC+∠OBC=180°.
【答案】见解析.
【解析】
如图,作CE⊥ON于E,CF⊥OM于F.由Rt△CFA≌Rt△CEB,推出∠ACF=∠ECB,推出∠ACB=∠ECF,由∠ECF+∠MON=360°﹣90°﹣90°=180°,可得∠ACB+∠AOB=180°,推出∠OAC+∠OBC=180°.
如图,作CE⊥ON于E,CF⊥OM于F.
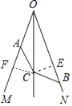
∵OC平分∠MON,CE⊥ON于E,CF⊥OM于F.
∴CE=CF,
∵AC=BC,∠CEB=∠CFA=90°,
∴Rt△CFA≌Rt△CEB(HL),
∴∠ACF=∠ECB,
∴∠ACB=∠ECF,
∵∠ECF+∠MON=360°﹣90°﹣90°=180°,
∴∠ACB+∠AOB=180°,
∴∠OAC+∠OBC=180°.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目