题目内容

【题目】如图，一个半径为r的圆形纸片在边长为a（ ）的等边三角形内任意运动，则在该等边三角形内，这个圆形纸片“不能接触到的部分”的面积是（ ）
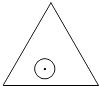
A.
B.
C.
D.πr2

【答案】C
【解析】如图，当圆形纸片运动到与A的两边相切的位置时，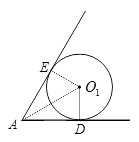

过圆形纸片的圆心O1作两边的垂线，垂足分别为D，E，
连接AO1，则RtADO1中，O1AD=30，O1D=r，AD=r，
∴SADO1=O1DAD=r2，由此S四边形ADO1E=2SADO1=r2，
∵由题意，DO1E=120，得S扇形O1DE=r2，
∴圆形纸片“不能接触到的部分”的面积是3（r2-r2）=（）r2 .
所以答案是：C.
【考点精析】认真审题，首先需要了解切线的性质定理(切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)．

练习册系列答案
相关题目

【题目】探究：如何把多项式x2+8x+15因式分解？

（1）观察：上式能否可直接利用完全平方公式进行因式分解？ 答： ；

（阅读与理解）：由多项式乘法，我们知道(x+a)(x+b)=x2+(a+b)x+ab，将该式从右到左地使用，即可对形如x2+(a+b)x+ab的多项式进行因式分解，即：

x2+(a+b)x+ab=(x+a)(x+b)

此类多项式x2+(a+b)x+ab的特征是二次项系数为1，常数项为两数之积，一次项系数为这两数之和．

（2）猜想并填空： x2+8x+15= x2+[( ) +( )]x + ( )×( )=(x+ )(x+ )

（3）上面多项式x2+8x+15的因式分解是否正确，我们需要验证．请写出验证过程．

（4）请运用上述方法将下列多项式进行因式分解：

① x2+8x+12 ② x2-x-12

【题目】已知点P为平面内一点，若点P 到⊙O上的点的最长距离为5，最短距离为1，则⊙O 的半径为 ．

【题目】（2015随州）甲骑摩托车从A地去B地，乙开汽车从B地去A地，同时出发，匀速行驶，各自到达终点后停止，设甲、乙两人间距离为s（单位：千米），甲行驶的时间为t（单位：小时），s与t之间的函数关系如图所示，有下列结论：

①出发1小时时，甲、乙在途中相遇；

②出发1.5小时时，乙比甲多行驶了60千米；

③出发3小时时，甲、乙同时到达终点；

④甲的速度是乙速度的一半．

其中，正确结论的个数是（　　）

A. 4 B. 3 C. 2 D. 1

【题目】如图，A（-5，0），B（-3，0），点C在y轴的正半轴上，∠CBO=45°，CD∥AB．∠CDA=90°．点P从点Q（4，0）出发，沿x轴向左以每秒1个单位长度的速度运动，运动时时间t秒．

（1）求点C的坐标；
（2）当∠BCP=15°时，求t的值；
（3）以点P为圆心，PC为半径的⊙P随点P的运动而变化，当⊙P与四边形ABCD的边（或边所在的直线）相切时，求t的值．

【题目】杨华与季红用5张同样规格的硬纸片做拼图游戏，正面如图1所示，背面完全一样，将它们背面朝上搅匀后，同时抽出两张．规则如下：当两张硬纸片上的图形可拼成电灯或小人时，杨华得1分；当两张硬纸片上的图形可拼成房子或小山时，季红得1分（如图2）．问题：游戏规则对双方公平吗？请说明理由；若你认为不公平，如何修改游戏规则才能使游戏对双方公平？

【题目】如图，一次函数图象经过点A（0，2），且与正比例函数y＝﹣x的图象交于点B，B点的横坐标是﹣1．

（1）求该一次函数的解析式：

（2）求一次函数图象、正比例函数图象与x轴围成的三角形的面积．

【题目】如图，△ABC在平面直角坐标系中，A（﹣2，5），B（﹣3，2），C（﹣1，1）．

（1）请画出△ABC关于y轴的对称图形△A′B′C′，其中A点的对应点是A′，B点的对应点是B′，C点的对应点是C′，并写出A′，B′，C′三点的坐标．

（2）求△A′B′C′的面积．

【题目】在等边三角形ABC中，AB=6，点D是BC边上的一点，点P是AB边上的一点，连接PD，以PD为边作等边三角形PDE，连接BE．

（1）如图1，当点P与点A重合时，

①找出图中的一对全等三角形，并证明；

②BE+BD=；

（2）如图2，若AP=1，请计算BE+BD的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网