Question

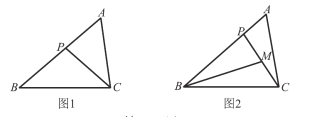
【题目】在△ABC中，P为边AB上一点．

(1)如图l，若∠ACP=∠B，求证：AC2 =AP·AB；

(2)若M为CP的中点，AC=2，如图2，若∠PBM=∠ACP，AB=3，求BP的长．

Answer 1

【答案】（1）证明见解析（2）

【解析】试题分析：

（1）由已知条件易证△ACP∽△ABC，由此可得AC:AB=AP:AC，即：AC2=AP·AB；

（2）过点C作CQ∥BM交AB延长线于Q，由平行线分线段成比例结合点M是PC的中点可得BP=BQ，设BP= ，则可得BQ = ，AP= ，AQ= ；再证△APC∽△ACQ可得AC2 =AP·AQ，即，解方程即可求得BP的长.

试题解析：

（1）∵∠ACP=∠B，∠BAC=∠CAP，

∴△ACP∽△ABC，

∴AC：AB=AP：AC，

∴AC2=AP·AB；

（2）如下图，作CQ∥BM交AB延长线于Q，

又∵点M是PC的中点，

∴PB：BQ=PM：MC=1，

设BP= ，则BQ = ，

∵AB=3，

∴AP= ，AQ= ，

∵∠PBM=∠ACP，∠PAC= ∠CAQ，

∴△APC∽△ACQ，

∴AC：AQ=AP：AC，

∴AC2 =AP·AQ，即，

解得： （不合题意，舍去），

即BP的长为.