��Ŀ����
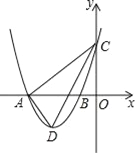
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+3��x�ύ��A����4��0����B����l��0�����㣬��y�ύ�ڵ�C����D�ǵ���������������һ���㣮
��1���������ߵĽ���ʽ��
��2�����D�ĺ�����Ϊm����ACD�����Ϊ�����S��m�ĺ�����ϵʽ����ȷ��mΪ��ֵʱS�����ֵ�����ֵ�Ƕ��٣�
��3������P�������߶Գ�����һ�㣬�Ƿ���ڵ�Pʹ����APC=90���������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=![]() x2+
x2+![]() x+3����2��mΪ��2ʱS�����ֵ�����ֵ��6��3��P������Ϊ����
x+3����2��mΪ��2ʱS�����ֵ�����ֵ��6��3��P������Ϊ����![]() ��
�� ![]() ����
����![]() ��
�� ![]() ��
��
�����������������(1)������A�͵�B������������ʽ�����ô���ϵ���������������ʽ��(2)�����������C�����꣬Ȼ�����ô���ϵ�������ֱ��AC�ĺ�������ʽ������D D��DE��y�ᣬ��AC�ڵ�E�������D�͵�E�����꣬Ȼ�����DE�ij��ȣ���������ļ��㹫ʽ�ó�����Ķ��κ�������ʽ���Ӷ��ó���������ֵ��(3)����ACΪֱ����Բ�������ߵĶԳ�����P�����ݵ�A �͵�C������ó��е�����꣬���AC��OP�ij��ȣ����P������Ϊ��![]() ��y����Ȼ����ݹ��ɶ������y��ֵ���ó���P�����꣮
��y����Ȼ����ݹ��ɶ������y��ֵ���ó���P�����꣮
���������(1)����A����4��0����B����l��0������y=ax2+bx+3�ã�![]() ��
��
���![]() �� �������ߵĺ�������ʽΪy=
�� �������ߵĺ�������ʽΪy=![]() x2+
x2+![]() x+3��
x+3��
(2)����x=0����y=3�� ��C��0��3����
��ֱ��AC�Ľ���ʽΪy=mx+n�� ����A����4��0����C��0��3����![]() �� ���
�� ���![]()
��AC�Ľ���ʽΪy=![]() x+3��
x+3��
��D��DE��y�ᣬ��AC�ڵ�E����D��m��![]() m2+
m2+![]() m+3����E��m��
m+3����E��m��![]() m+3������4��m����1���� ��DE=
m+3������4��m����1���� ��DE=![]() m+3����
m+3����![]() m2+
m2+![]() m+3���� ��DE=��
m+3���� ��DE=��![]() m2��3m��
m2��3m��
��S=![]() DE��4=2����
DE��4=2����![]() m2��3m��=��
m2��3m��=��![]() m2��6m=��
m2��6m=��![]() ��m+2��2+6��
��m+2��2+6��
��m=��2ʱ��S���=6�� ��mΪ��2ʱS�����ֵ�����ֵ��6��
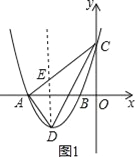
(3)�����ڵ�Pʹ����APC=90�㣬 ��ACΪֱ����Բ�������ߵĶԳ�����P��
��A����4��0����C��0��3���� ��AC���е�O������Ϊ����2��![]() ����AC=
����AC=![]() =5��
=5��
��OP=![]() =
=![]() �� ��������y=ax2+bx+3��x�ύ��A����4��0����B����l��0�����㣬
�� ��������y=ax2+bx+3��x�ύ��A����4��0����B����l��0�����㣬
���Գ���x=![]() =��
=��![]() �� ��P����
�� ��P����![]() ��y���� ��OP2=��
��y���� ��OP2=��![]() ��2��
��2��
������2+![]() ��2+��
��2+��![]() ��y��2=��
��y��2=��![]() ��2�� ���y=
��2�� ���y=![]() ��
��![]() ��
��
��P����������![]() ��
��![]() ����
����![]() ��
��![]() ����
����