题目内容
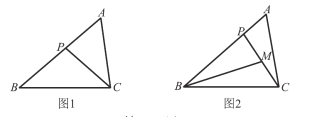
【题目】如图,在![]() 中,
中,![]() .
.

(1)证明:![]() ;
;
(2)![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据三角形的一个外角等于与它不相邻的两个内角的和得出∠3+∠CAE=∠DEF,再根据∠1=∠3整理即可得证;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和得出∠2+∠BCF=∠DFE,再根据∠2=∠3即可得∠ACB=∠DFE,然后利用三角形的内角和等于180°求解即可.
(1)证明:在△ACE中,∠DEF=∠3+∠CAE,
∵∠1=∠3,
∴∠DEF=∠1+∠CAE=∠BAC,
即∠BAC=∠DEF;
(2)解:在△BCF中,∠DFE=∠2+∠BCF,
∵∠2=∠3,
∴∠DFE=∠3+∠BCF,
即∠DFE=∠ACB,
∵∠BAC=70°,∠DFE=50°,
∴在△ABC中,∠ABC=180°-∠BAC-∠ACB=180°-70°-50°=60°.

练习册系列答案
相关题目
【题目】某村庄计划建造A,B两种型号的沼气池共20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积和可供使用农户数见下表:
型号 | 占地面积 (单位:m2/个) | 可供使用农户数 (单位:户/个) |
A | 15 | 18 |
B | 20 | 30 |
已知可供建造沼气池的占地面积不超过365m2,该村农户共有492户.
(1)如何合理分配建造A,B型号“沼气池”的个数才能满足条件?满足条件的方案有几种?通过计算分别写出各种方案.
(2)请写出建造A、B两种型号的“沼气池”的总费用y和建造A型“沼气池”个数x之间的函数关系式;
(3)若A型号“沼气池”每个造价2万元,B型号“沼气池”每个造价3万元,试说明在(1)中的各种建造方案中,哪种建造方案最省钱,最少的费用需要多少万元?