Question

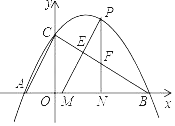
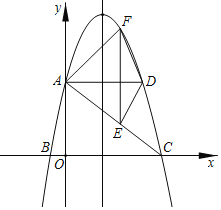
【题目】如图，在平面直角坐标系中，抛物线y＝﹣x2+4x+5与y轴交于点A，与x轴的正半轴交于点C.

(1)求直线AC解析式；

(2)过点A作AD平行于x轴，交抛物线于点D，点F为抛物线上的一点(点F在AD上方)，作EF平行于y轴交AC于点E，当四边形AFDE的面积最大时？求点F的坐标，并求出最大面积；

(3)若动点P先从(2)中的点F出发沿适当的路径运动到抛物线对称轴上点M处，再沿垂直于y轴的方向运动到y轴上的点N处，然后沿适当的路径运动到点C停止，当动点P的运动路径最短时，求点N的坐标，并求最短路径长.

Answer 1

【答案】(1)y＝﹣x+5；(2)点F(，)；四边形AFDE的面积的最大值为；(3)点N(0，)，点P的运动路径最短距离＝2+.

【解析】

(1)先求出点A，点C坐标，用待定系数法可求解析式；

(2)先求出点D坐标，设点F(x，﹣x2+4x+5)，则点E坐标为(x，﹣x+5)，即可求EF＝﹣x2+5x，可求四边形AFDE的面积，由二次函数的性质可求解；

(3)由动点P的运动路径＝FM+MN+NC＝GM+2+MH，则当点G，点M，点H三点共线时，动点P的运动路径最小，由两点距离公式可求解.

解：(1)∵抛物线y＝﹣x2+4x+5与y轴交于点A，与x轴的正半轴交于点C.

∴当x＝0时，y＝5，则点A(0，5)

当y＝0时，0＝﹣x2+4x+5，

∴x1＝5，x2＝﹣1，

∴点B(﹣1，0)，点 C(5，0)

设直线AC解析式为：y＝kx+b，

∴

解得：

∴直线AC解析式为：y＝﹣x+5，

(2)∵过点A作AD平行于x轴，

∴点D纵坐标为5，

∴5＝﹣x2+4x+5，

∴x1＝0，x2＝4，

∴点D(4，5)，

∴AD＝4

设点F(x，﹣x2+4x+5)，则点E坐标为(x，﹣x+5)

∴EF＝﹣x2+4x+5﹣(﹣x+5)＝﹣x2+5x，

∵四边形AFDE的面积＝AD×EF＝2EF＝﹣2x2+10x＝﹣2(x﹣)2+

∴当x＝时，四边形AFDE的面积的最大值为，

∴点F(，)；

(3)∵抛物线y＝﹣x2+4x+5＝﹣(x﹣2)2+9，

∴对称轴为x＝2，

∴MN＝2，

如图，将点C向右平移2个单位到点H(7，0)，过点F作对称轴x＝2的对称点G(，)，连接GH，交直线x＝2于点M，

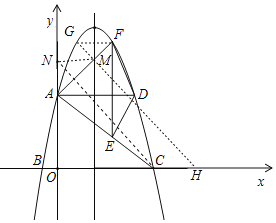
∵MN∥CH，MN＝CH＝2，

∴四边形MNCH是平行四边形，

∴NC＝MH，

∵动点P的运动路径＝FM+MN+NC＝GM+2+MH，

∴当点G，点M，点H三点共线时，动点P的运动路径最小，

∴动点P的运动路径最短距离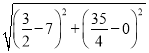＝2+＝2+，

设直线GH解析式为：y＝mx+n，

∴，

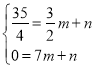解得，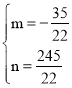

∴直线GH解析式为：y＝﹣x+，

当x＝2时，y＝，

∴点N(0，).