Question

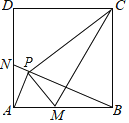
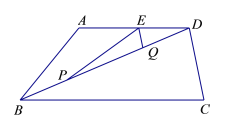
【题目】如图，在梯形ABCD中，AD∥BC，BC=BD=10，CD=4，AD=6．点P是线段BD上的动点，点E、Q分别是线段DA、BD上的点，且DE=DQ=BP，联结EP、EQ．

（1）求证：EQ∥DC；

（2）如果△EPQ是以EQ为腰的等腰三角形，求线段BP的长；

（3）当BP=m（0<m<5）时，求∠PEQ的正切值．（用含m的式子表示）

Answer 1

【答案】（1）见解析；（2）；（3）.

【解析】

（1）利用两边成比例且夹角相等可判定△DEQ ∽△BCD，从而证得结论；

（2）设BP的长为x，则DQ=x，QP=2x-10，利用（1）的结论△DEQ ∽△BCD，求得．分类讨论：当EQ=EP、QE=QP时，分别求得答案即可；

（3）过点P作PH⊥EQ，交EQ的延长线于点H；过点B作BG⊥DC，垂足为点G，易证得△PHQ ∽△BGD，利用对应边成比例通过计算得到的值，从而求得答案.

（1）∵AD//BC，∴∠EDQ=∠DBC．

∵，，∴．

∴△DEQ ∽△BCD．

∴∠DQE=∠BDC，

∴EQ//CD．

（2）设BP的长为x，则DQ=x，QP=2x-10．

∵△DEQ ∽△BCD，

∴，

∴．

（i）当EQ=EP时，

∴∠EQP =∠EPQ，

∵DE=DQ，∴∠EQP =∠QED，∴∠EPQ =∠QED，

∴△EQP ∽△DEQ，∴，∴，

解得 ，或（舍去）．

（ii）当QE=QP时，

∴，解得 ，

∵，∴此种情况不存在．

∴

（3）过点P作PH⊥EQ，交EQ的延长线于点H；过点B作BG⊥DC，垂足为点G．

∵BD=BC，BG⊥DC，∴DG=2，BG，

∵BP= DQ=m，∴PQ=10-2m．

∵EQ∥DC∴∠PQH =∠BDG．

又∵∠PHQ =∠BGD= 90°，

∴△PHQ ∽△BGD．

∴，∴．

∴，．

∴，

∴