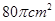题目内容
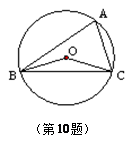
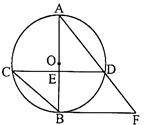
如图,以AB为直径的⊙O经过点C,D是AB延长线上一点,且DC=AC,∠CAB=30°
小题1:试判断CD所在的直线与⊙O的位置关系,并说明理由
小题2:若AB=2,求阴影部分的面积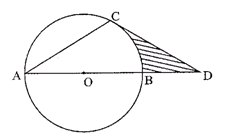
小题1:试判断CD所在的直线与⊙O的位置关系,并说明理由
小题2:若AB=2,求阴影部分的面积

小题1:CD与⊙O相切 ……………………………………………………… 1分
理由如下:连接OC
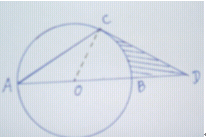
∵OA=OC,∠CAB=30°……………… 2分
∴∠ACO=∠CAB=30°
又∵AC=BC,∴∠ACD=180°-2∠CAB=120°… 3分
∴∠OCD=∠ACD-∠ACO=120°-30°=90°
∴CD与⊙O相切 ……………………… 5分
小题2:∵∠COD=2∠CAB=60°,OC=
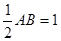 ……………………………………… 6分
……………………………………… 6分在Rt△OCD中,CD=OC×tan60°=
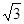 ………………………………………… 7分
………………………………………… 7分∴
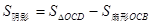 ……………………………………………………… 8分
……………………………………………………… 8分=
 …………………………………… 10分
…………………………………… 10分(1)连接OC,证明∠OCD=90°,从而判断CD与⊙O相切.易证∠A=30°,∠OCD=90°,从而得证;
(2)根据图中阴影部分的面积等于S△OCD-S扇形OCB可得出答案.
(2)根据图中阴影部分的面积等于S△OCD-S扇形OCB可得出答案.

练习册系列答案
相关题目
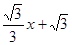 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O,若将⊙P沿x轴向左平平移,当⊙P向左平移 个单位长度时,⊙P与该直线相切.
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O,若将⊙P沿x轴向左平平移,当⊙P向左平移 个单位长度时,⊙P与该直线相切. 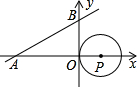
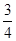 ,求线段AD、CD的长.
,求线段AD、CD的长.
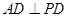 (2)若圆的半径为1,△ABE是等边三角形,求BP的长.
(2)若圆的半径为1,△ABE是等边三角形,求BP的长.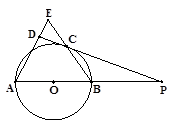
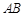 、
、 相交于点
相交于点 ,若
,若 ,
,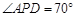 ,则
,则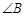 等于( )
等于( )