Question

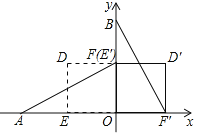
【题目】在平面直角坐标系中，O为原点，点A（﹣2，0），点B（0，2），点E，点F分别为OA，OB的中点．若正方形OEDF绕点O顺时针旋转，得正方形OE′D′F′，记旋转角为α．当α=90°时，求AE′，BF′的长．

Answer 1

【答案】AE′，BF′的长都为．

【解析】

试题分析：根据点A和点B的坐标得到OA=2，OE=1，OB=2，OF=1，再根据旋转的性质得E′（0，1），F′（1，0），然后利用勾股定理计算AE′，BF′的长．

解：∵点A（﹣2，0），点B（0，2），点E，点F分别为OA，OB的中点，

∴OA=2，OE=1，OB=2，OF=1，

∵正方形OEDF绕点O顺时针旋转90°，得正方形OE′D′F′，

∴E′（0，1），F′（1，0），

在Rt△OAE′中，AE′===；

在Rt△OBF′中，BF′===．

即AE′，BF′的长都为．