题目内容
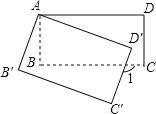
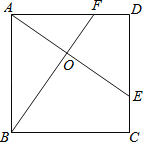
【题目】如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)S△AOB=S四边形DEOF中正确的有( )
A.4个 B.3个 C.2个 D.1个
【答案】B
【解析】
试题分析:根据正方形的性质得AB=AD=DC,∠BAD=∠D=90°,则由CE=DF易得AF=DE,根据“SAS”可判断△ABF≌△DAE,所以AE=BF;根据全等的性质得∠ABF=∠EAD,
利用∠EAD+∠EAB=90°得到∠ABF+∠EAB=90°,则AE⊥BF;连结BE,BE>BC,BA≠BE,而BO⊥AE,根据垂直平分线的性质得到OA≠OE;最后根据△ABF≌△DAE得S△ABF=S△DAE,则S△ABF﹣S△AOF=S△DAE﹣S△AOF,即S△AOB=S四边形DEOF.
解:∵四边形ABCD为正方形,
∴AB=AD=DC,∠BAD=∠D=90°,
而CE=DF,
∴AF=DE,
在△ABF和△DAE中
 ,
,
∴△ABF≌△DAE,
∴AE=BF,所以(1)正确;
∴∠ABF=∠EAD,
而∠EAD+∠EAB=90°,
∴∠ABF+∠EAB=90°,
∴∠AOB=90°,
∴AE⊥BF,所以(2)正确;
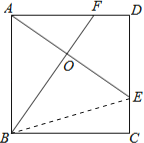
连结BE,
∵BE>BC,
∴BA≠BE,
而BO⊥AE,
∴OA≠OE,所以(3)错误;
∵△ABF≌△DAE,
∴S△ABF=S△DAE,
∴S△ABF﹣S△AOF=S△DAE﹣S△AOF,
∴S△AOB=S四边形DEOF,所以(4)正确.
故选:B.

练习册系列答案
相关题目