题目内容
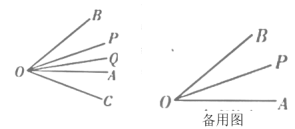
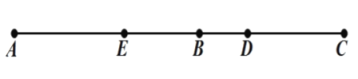
【题目】如图,![]() 为线段
为线段![]() 上靠近点
上靠近点![]() 的三等分点,
的三等分点,![]() 为线段
为线段![]() 上的两点,且满足
上的两点,且满足![]() .
.
(1)若![]() ,求线段
,求线段![]() 的长.
的长.
(2)若图中所有线段的长度之和是线段![]() 长度的
长度的![]() 倍,求
倍,求![]() 的值.
的值.
(3)若![]() ,动点
,动点![]() 从
从![]() 点、动点
点、动点![]() 从
从![]() 点同时出发,分别以
点同时出发,分别以![]() 的速度沿直线
的速度沿直线![]() 向右运动,是否存在某个时刻使得
向右运动,是否存在某个时刻使得![]() 成立?若存在,求此时
成立?若存在,求此时![]() 的长度;若不存在,说明理由.
的长度;若不存在,说明理由.
【答案】(1)9;(2)3;(3)存在,PQ=9或0
【解析】
(1)令![]() ,可得
,可得![]() ,再根据
,再根据![]() ,可求出
,可求出![]() ,根据
,根据![]() 即可求出线段
即可求出线段![]() 的长.
的长.
(2)设![]() ,即
,即![]() ,根据图中所有线段之和是
,根据图中所有线段之和是![]() 长度
长度![]() 倍列出方程,可得
倍列出方程,可得![]() ,即可得出
,即可得出![]() 的值.
的值.
(3)分三种情况:①![]() 在
在![]() 左边时,
左边时,![]() ;②
;②![]() 在
在![]() 右边,
右边,![]() 在
在![]() 左边时,
左边时,![]() ;③
;③![]() 在
在![]() 右边时且
右边时且![]() 在
在![]() 右边时,
右边时,![]() ,列出方程求解即可.
,列出方程求解即可.
(1)令![]() ,
,![]() ,
,
∵![]()
![]()
又![]()
![]()
![]()
![]()
(2)设![]()
![]()
则:图中所有线段之和是![]() 长度
长度![]() 倍
倍
![]()
整理得![]()
![]()
![]()
![]()
(3)①![]() 在
在![]() 左边时,
左边时,![]()
![]()
![]()
解得![]()
此时![]()
②![]() 在
在![]() 右边,
右边,![]() 在
在![]() 左边时,
左边时,![]()
![]()
![]()
解得![]() (舍)
(舍)
③![]() 在
在![]() 右边时且
右边时且![]() 在
在![]() 右边时,
右边时,![]()
![]()
![]()
解得![]()
此时![]()

练习册系列答案
相关题目