题目内容
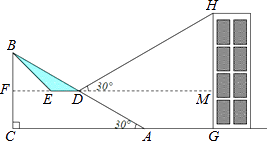
【题目】如图 1,在平面直角坐标系中,点 A 为 x 轴负半轴上一点,点 B 为 x 轴正半轴上一点,C(0,﹣2),D(﹣3,﹣2).


(1)AB,CD 的位置关系为 ;△BCD 的面积为 ;S△ACD S△BCD(填两者之间的数量关系);
(2)如图 1,若∠1=100°,∠ACB=65°,求∠CAB 的度数;
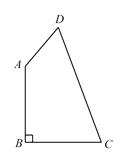
(3)如图 2,若∠ADC=∠DAC,∠ACB 的平分线 CE 交 DA 的延长线于点 E,在 B 点的运动过程中![]() 的值是否变化?若不变,直接写出其值;若变化,请说明理由.(注:三角形内角和等于 180°)
的值是否变化?若不变,直接写出其值;若变化,请说明理由.(注:三角形内角和等于 180°)
【答案】(1)平行,3,=;(2)∠CAB=35°;(3)在B点的运动过程中,∠E与∠ABC的比值不变.![]() .
.
【解析】
(1)根据纵坐标相等的点,所在直线平行于x轴即可得出AB,CD的位置关系,再根据平行线的性质可得△BCD的面积和S△ACD与S△BCD的面积关系;
(2)利用三角形的外角的性质即可解决问题;
(3)设EC交AB于F.∠ADC=∠DAC=α,∠ACE=β,想办法求出∠E,∠ABC(用α,β表示),即可解决问题.
(1)∵C(0,﹣2),D(﹣3,﹣2),
∴CD∥AB,
∴S△BCD=![]() ×3×2=3,S△ACD=S△BCD,
×3×2=3,S△ACD=S△BCD,
故答案为平行,3,=.
(2)如图1中,

∵∠1=180° -∠ABC, ∠CAB+∠ACB=180° -∠ABC,
∴∠1=∠CAB+∠ACB,
∵∠1=100°,∠ACB=65°,
∴∠CAB=100°﹣65°=35°.
(3)在B点的运动过程中,∠E与∠ABC的比值不变.
理由如下:设EC交AB于F.∠ADC=∠DAC=α,∠ACE=β,

在△ACE中,∠E=α﹣β,
在△AFE和△BFC中,∠E+∠EAF+∠AFE=180°,
∠ABC+∠BCF+∠BFC=180°,
∵CD∥x轴,
∴∠EAO=∠ADC,
又∵∠AFE=∠BFC(对顶角相等),
∴∠E+∠EAO=∠ABC+∠BCF,
α﹣β+α=∠ABC+β,
∴∠ABC=2(α﹣β),
∴![]() .
.
即在B点的运动过程中,∠E与∠ABC的比值不变.

 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案