题目内容
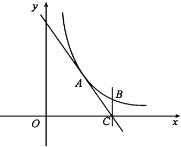
【题目】如图，反比例函数y=
（x＞0）过点A（3，4），直线AC与x轴交于点C（6，0），过点C作x轴的垂线BC交反比例函数图象于点B.
（1）求k的值与B点的坐标；
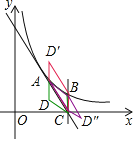
（2）在平面内有点D，使得以A，B，C，D四点为顶点的四边形为平行四边形，试写出符合条件的所有D点的坐标.
【答案】（1）k=12，B（6，2）；（2）D1（3，2）或D2（3，6）或D3（9，-2）.
【解析】（1）将A点的坐标代入反比例函数y=
求得k的值，然后将x=6代入反比例函数解析式求得相应的y的值，即得点B的坐标；
（2）使得以A、B、C、D为顶点的四边形为平行四边形，如图所示，找出满足题意D的坐标即可．
（1）把点A（3，4）代入y=（x＞0），得
k=xy=3×4=12，
故该反比例函数解析式为：y=
．
∵点C（6，0），BC⊥x轴，
∴把x=6代入反比例函数y=，得
y==2．
则B（6，2）．
综上所述，k的值是12，B点的坐标是（6，2）．
（2）①如图，当四边形ABCD为平行四边形时，AD∥BC且AD=BC．
∵A（3，4）、B（6，2）、C（6，0），
∴点D的横坐标为3，yA-yD=yB-yC即4-yD=2-0，故yD=2．
所以D（3，2）．
②如图，当四边形ACBD′为平行四边形时，AD′∥CB且AD′=CB．
∵A（3，4）、B（6，2）、C（6，0），
∴点D的横坐标为3，yD′-yA=yB-yC即yD-4=2-0，故yD′=6．
所以D′（3，6）．
③如图，当四边形ACD″B为平行四边形时，AC=BD″且AC=BD″．
∵A（3，4）、B（6，2）、C（6，0），
∴xD″-xB=xC-xA即xD″-6=6-3，故xD″=9．
yD″-yB=yC-yA即yD″-2=0-4，故yD″=-2．
所以D″（9，-2）．
综上所述，符合条件的点D的坐标是：（3，2）或（3，6）或（9，-2）．
