��Ŀ����
����Ŀ��һ�������������������ֲ�������̽�����������������Ĺ��̣�������һ��������������һ��.
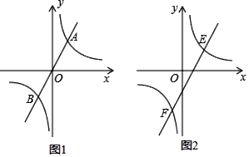
�����ֲ��룩��1����ͼ�٣���֪��AOB��70������AOD��100����OCΪ��BOD�Ľ�ƽ���ߣ����AOC�Ķ���Ϊ ��.


��̽�����ɣ���2����ͼ�٣���AOB��m����AOD��n��OCΪ��BOD�Ľ�ƽ����. �����AOC�Ķ������ú�m��n�Ĵ���ʽ��ʾ������˵������.
������������3����ͼ�ڣ�����AOB��20������AOC��90������AOD��120��.������OB�Ƶ�O��ÿ��20����ʱ����ת������OC�Ƶ�O��ÿ��10��˳ʱ����ת������OD�Ƶ�Oÿ��30��˳ʱ����ת����������ͬʱ��ת����һ��������ֱ��OA�غ�ʱ����������ͬʱֹͣ�˶�. �˶�����ʱ������һ�������������������нǵĽ�ƽ���ߣ�
���𰸡���1��85������2����AOC��![]() �����ɼ���������3������
�����ɼ���������3������![]() ��
��![]() ��4��ʱ������һ�������������������нǵ�ƽ����.
��4��ʱ������һ�������������������нǵ�ƽ����.
��������
��1�����ݡ�AOD����AOB����BOD֮��Ĺ�ϵ�������BOD�Ķ�����Ȼ����ݽ�ƽ���ߵ����������BOC�Ķ������ټ����AOC���ɽ������.
��2�����ݡ�AOD����AOB����BOD֮��Ĺ�ϵ����m��n��ʾ����BOD�Ķ�����Ȼ����ݽ�ƽ���ߵ�������m��n�Ĵ���ʽ��ʾ����BOC������ٱ�ʾ����AOC���ɽ������.
��3�����ݸ���֮����ڵ�������ϵ���辭��x��ʱ���ֱ���x����DOA����COA����BOA��ʾ������Ȼ�������������ۣ����ݽ�ƽ���ߵ������г����̣��������.
��1��85����
��2���ߡ�AOB��m����AOD��n
���BOD��n��m
��OCΪ��BOD�Ľ�ƽ����
���BOC��![]()
���AOC��![]() +m��
+m��![]()
��3���辭����ʱ��Ϊx�룬
���DOA��120����30x����COA��90����10x����BOA��20��+20x��
�ٵ���x��![]() ֮ǰ��OCΪOB��OD�Ľ�ƽ���ߣ�30��20x��70��30x��x1��4���ᣩ��
֮ǰ��OCΪOB��OD�Ľ�ƽ���ߣ�30��20x��70��30x��x1��4���ᣩ��
�ڵ�x��![]() ��2֮�䣬ODΪOC��OB�Ľ�ƽ���ߣ���30+20x��100��50x��x2��
��2֮�䣬ODΪOC��OB�Ľ�ƽ���ߣ���30+20x��100��50x��x2��![]() ��
��
�۵�x��2��![]() ֮�䣬OBΪOC��OD�Ľ�ƽ���ߣ�70��30x����100+50x��x3��
֮�䣬OBΪOC��OD�Ľ�ƽ���ߣ�70��30x����100+50x��x3��![]() ��
��
�ܵ�x��![]() ��4֮�䣬OCΪOB��OD�Ľ�ƽ���ߣ���70+30x����30+20x��x4��4.
��4֮�䣬OCΪOB��OD�Ľ�ƽ���ߣ���70+30x����30+20x��x4��4.
�𣺾���![]() ��
��![]() ��4��ʱ������һ�������������������нǵ�ƽ����.
��4��ʱ������һ�������������������нǵ�ƽ����.

����Ŀ��ij������˾����114�ֻ���ƻ�ͬʱ���A��B�����ͺŵij�������������һ���˻������ϵ�һ����Ϣ�ǣ�
A�ͳ������أ� | B�ͳ������أ� | �˻����� |
3�� | 2�� | 38�� |
1�� | 3�� | 36�� |
����������Ϣ�������������⣺
��1��1��A�ͳ���1��B�ͳ���װ������һ�οɷֱ��˻����ٶ֣�
��2����������˾����һ�����꣬��ǡ��ÿ������װ�����������������˾����������