��Ŀ����
����Ŀ��ij�����Ϊ�������˿ͣ���A��B���ֵ����У�������������һ�ֵ���۸������γ�����ӯ��ģʽ��ģʽһ��A�ֵ�������ÿ��8Ԫ��B�ֵ�������ÿ��15Ԫ��ģʽ����A�ֵ�������ÿ��14Ԫ��B�ֵ�������ÿ��11Ԫÿ��������A��B���ֵ��40�У��Ҷ������꣬��ÿ������A�ֵ���x��
��1���谴ģʽһ����A��B���ֵ�����������Ϊy1Ԫ����ģʽ������A��B���ֵ�����������Ϊy2Ԫ���ֱ����y1��y2����x�ĺ�������ʽ��
��2����ͬһ������ϵ�ڷֱ�(1)���е�����������ͼ��

��3����yʼ�ձ�ʾy1��y2�нϴ��ֵ������y�Ƿ�Ϊx�ĺ�������˵˵������ɣ���ֱ��д��y����Сֵ��
���𰸡���1��y1==-7x+600��y2==3x+440 ��2���𰸼����� ��3���𰸼�����
��������
��1����������ӯ��ģʽ���ֱ��г�y1��y2����x�ĺ�������ʽ��
��2��������㷨����������ͼ��
��3����y1=y2����������x�ķ��̣��ⷽ�����x��ֵ���Ϳɵõ��������Ľ������꣬������һ�κ��������ʣ��Ϳɵó���0��x��40ʱ��y1��x�����������y2��x���������С���ɵõ�ÿһ���Ա���x����Ψһ��һ��y��ֵ��֮��Ӧ���ɴ˿ɵó��ж�.
��1���⣺ ������ã�
y1=8x+15��40-x��=-7x+600��
y2=14x+11��40-x��=3x+440 ��
��2���⣺ ��ͼ��
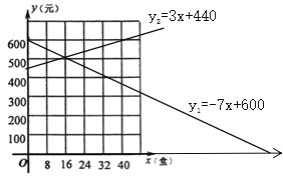
��3���⣺ ��y1=y2ʱ��-7x+600=3x+440
��֮��x=16
��x=16ʱ��y=3��16+440=488
��0��x��40ʱ��y1��x�����������y2��x���������С��
��![]()
��ÿһ���Ա���x����Ψһ��һ��y��ֵ��֮��Ӧ��
��y��x�ĺ�������x=16ʱ��y����СֵΪ488.

 ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�