题目内容
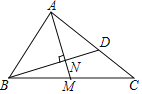
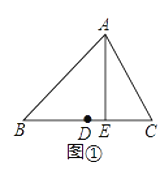
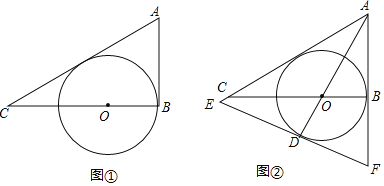
【题目】如图①,Rt△ABC中,∠ABC=90°,∠CAB的平分线交BC于点O,以O为圆心,OB长为半径作⊙O.
(1)求证:⊙O与AC相切.
(2)若AB=6,AC=10.
①求⊙O的半径;
②如图②,延长AO交⊙O于点D,过点D作⊙O的切线,分别交AC、AB的延长线于E、F,试求EF的长.
【答案】(1)见解析;(2)①![]() ;②
;②![]()
【解析】
(1)根据角平分线的性质,可以证明本结论成立;
(2)①根据切线的性质可知AB=AM,根据勾股定理可以求得BC的长,进而可以求得圆的半径的长;
②根据题意可以求得AD的长,然后根据三角形相似可以求得DF的长,由等腰三角形的性质可以求得EF的长.
(1)证明:∵∠ABC=90°,∠CAB的平分线是AO,
∴点O到AB和到AC的距离相等,
∴点O到AC的距离等于圆O的半径,
∴⊙O与AC相切;
(2)①作OM⊥AC于点M,如图所示,

∵AB=6,AC=10,∠ABC=90°,
∴BC=8,AB=AM=6,
∴MC=4,OC=8-OB,
设圆O的半径是r,
∴r2+42=(8-r)2
解得,r=3,
即⊙O的半径是3;
②∵AB=6,BO=3,∠ABO=90°,
∴AO=3![]() ,
,
∴AD=3+3![]() ,
,
∵AD⊥EF,
∴∠ADF=90°,
∴∠ADF=∠ABO=90°,
∵∠DAF=∠BAO,
∴△DAF∽△BAO,
∴![]() ,
,
即![]() ,
,
解得,DF=![]() ,
,
∵AD平分∠EAF,AD⊥EF,
∴EF=2DF=3+3![]() .
.

 应用题作业本系列答案
应用题作业本系列答案【题目】为了传承优秀传统文化,我市组织了一次初三年级1 200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:
成绩(分) | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
人数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |

成绩分组 | 频数 | 频率(百分比) |
35≤x<38 | 3 | 0.03 |
38≤x<41 | a | 0.12 |
41≤x<44 | 20 | 0.20 |
44≤x<47 | 35 | 0.35 |
47≤x≤50 | 30 | b |
请根据所提供的信息解答下列问题:
(1)频率统计表中a=________,b=_______;
(2)请补全频数分布直方图;
(3)请根据抽样统计结果,估计该次大赛中成绩不低于41分的学生有多少人?