题目内容
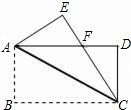
如图，在长方形ABCD中，AB=3厘米．在CD边上找一点E，沿直线AE把△ADE折叠，若点D恰好落在BC边上点F处，且△ABF的面积是6平方厘米，则DE的长为（ ）分析：先根据直角三角形的面积公式求得BF=4厘米，再根据勾股定理求得AF=5厘米，根据折叠的性质，得AD=AF=5厘米，则CF=1厘米．设DE=x，则EF=DE=x，CE=3-x，再根据勾股定理列方程求解．
解答：解：∵△AEF是△ADE沿直线AE翻折变换而成，
∴△AEF≌△ADE，
∴AF=AD，
∵四边形ABCD是矩形，
∴AD=BC，
∴AF=AD=BC，
∵AB=3厘米，△ABF的面积是6平方厘米，
∴
AB•BF=
×3BF=6，
∴BF=4（厘米），在Rt△ABF中，
AF=
=5厘米．则CF=AF-BF=1（厘米）
设DE=x，则EF=DE=x，CE=3-x，
在Rt△EFC中，根据勾股定理，得
1+（3-x）2=x2，
解得，x=
，即DE=
厘米．
故选D．
解：∵△AEF是△ADE沿直线AE翻折变换而成，∴△AEF≌△ADE，
∴AF=AD，
∵四边形ABCD是矩形，
∴AD=BC，
∴AF=AD=BC，
∵AB=3厘米，△ABF的面积是6平方厘米，
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴BF=4（厘米），在Rt△ABF中，
AF=
| AB2+BF2 |
设DE=x，则EF=DE=x，CE=3-x，
在Rt△EFC中，根据勾股定理，得
1+（3-x）2=x2，
解得，x=
| 5 |
| 3 |
| 5 |
| 3 |
故选D．
点评：此题综合考查了矩形的性质、勾股定理以及折叠的性质，善于运用勾股定理构造方程求解．
练习册系列答案
相关题目
于点F．
如图，在Rt△ABC中，∠ABC=90°，∠C=60°，BC=2，D是AC的中点，以D作DE⊥AC与CB的延长线交于E，以AB、BE为邻边作长方形ABEF，连接DF，求DF的长．
