题目内容
如图,在长方形ABCD(对边相等,四角都是直角)中,将△ABC沿AC对折至△AEC位置,CE与AD交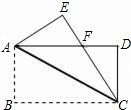 于点F.
于点F.(1)求证:△AFC是等腰三角形;
(2)若∠ACB=30°,BC=12cm,求DF的长.
分析:(1)由折叠的性质可知∠ECA=∠BCA,由AD∥BC可知∠DAC=∠BCA,则∠ECA=∠DAC,可证△AFC是等腰三角形;
(2)在Rt△ABC中,BC=12,∠ACB=30°,可求AB的长,由矩形性质得CD=AB,由折叠的性质可知∠ECA=∠ACB=30°,利用互余关系可求∠DCF=30°,在Rt△CDF中求DF即可.
(2)在Rt△ABC中,BC=12,∠ACB=30°,可求AB的长,由矩形性质得CD=AB,由折叠的性质可知∠ECA=∠ACB=30°,利用互余关系可求∠DCF=30°,在Rt△CDF中求DF即可.
解答:(1)证明:由折叠的性质可知∠ECA=∠BCA,
由AD∥BC可知∠DAC=∠BCA,
∴∠ECA=∠DAC,
∴△AFC是等腰三角形;
(2)解:∵在Rt△ABC中,BC=12,∠ACB=30°,
∴AB=BC•tan∠ACB=12×
=4
,
∴CD=AB=4
,
由折叠的性质可知∠ECA=∠ACB=30°,
∴∠DCF=90°-∠ECA-∠ACB=30°,
在Rt△CDF中,
DF=CD•tan∠DCF=4
×
=4.
由AD∥BC可知∠DAC=∠BCA,
∴∠ECA=∠DAC,
∴△AFC是等腰三角形;
(2)解:∵在Rt△ABC中,BC=12,∠ACB=30°,
∴AB=BC•tan∠ACB=12×
| ||
| 3 |
| 3 |
∴CD=AB=4
| 3 |
由折叠的性质可知∠ECA=∠ACB=30°,
∴∠DCF=90°-∠ECA-∠ACB=30°,
在Rt△CDF中,
DF=CD•tan∠DCF=4
| 3 |
| ||
| 3 |
点评:本题考查了折叠的性质,平行线的性质的运用,解直角三角形的有关知识.关键是利用折叠的性质将角、边进行转化.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.
如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.

