题目内容
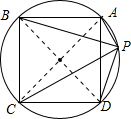
如图，⊙O是边长为1的正方形ABCD的外接圆，P为弧AD上的不同于A、D的任意一点，则PA2+PB2+PC2+PD2的值为（ ）
| A．2 | B．4 | C．6 | D．8 |
连接AC、BD．
∵ABCD是正方形，
∴∠ADC=∠BCD=90°，
∴AC与BD是直径，
∴∠APC=∠BPD=90°，
∴PA2+PC2=AC2，PB2+PD2=BD2．
又∵正方形ABCD的边长为1，
∴AC=BD=
，
∴PA2+PB2+PC2+PD2=AC2+BD2=4．
故选B．
∵ABCD是正方形，
∴∠ADC=∠BCD=90°，
∴AC与BD是直径，
∴∠APC=∠BPD=90°，
∴PA2+PC2=AC2，PB2+PD2=BD2．
又∵正方形ABCD的边长为1，
∴AC=BD=
| 2 |
∴PA2+PB2+PC2+PD2=AC2+BD2=4．
故选B．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
