题目内容
【题目】某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,
组别 | 课堂发言次数n |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
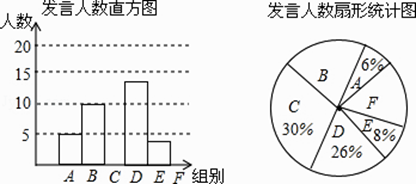
请结合图中相关数据回答下列问题:
(1)样本容量是 , 并补全直方图;
(2)该年级共有学生800人,请估计该年级在这天里发言次数不少于12次的人数;
(3)已知A组发言的学生中恰好有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好都是男生的概率.
【答案】
(1)50;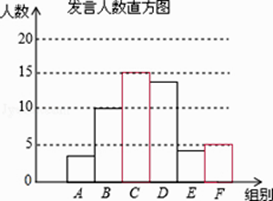
(2)解:F组发言的人数所占的百分比为:10%,
所以,估计全年级在这天里发言次数不少于12次的人数为:800×(8%+10%)=144(人)
(3)解:∵A组发言的学生为:50×6%=3人,有1位女生,
∴A组发言的有2位男生,
∵E组发言的学生:4人,
∴有2位女生,2位男生.
∴由题意可画树状图为:
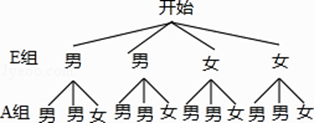
∴共有12种情况,所抽的两位学生恰都是男生的情况有4种,
∴所抽的两位学生恰好是一男一女的概率为 ![]() =
= ![]()
【解析】解:(1)∵B、E两组发言人数的比为5:2,E组发言人数占8%, ∴B组发言的人数占20%,
由直方图可知B组人数为10人,
所以,被抽查的学生人数为:10÷20%=50人,
∴样本容量为50人.
F组人数为:50×(1﹣6%﹣20%﹣30%﹣26%﹣8%)
=50×(1﹣90%)
=50×10%,
=5(人),
C组人数为:50×30%=15(人),
E组人数为:50×8%=4人
补全的直方图如图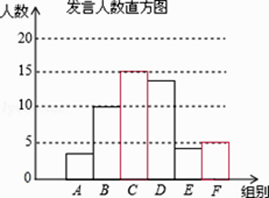 ;
;
【考点精析】本题主要考查了总体、个体、样本、样本容量和频数分布直方图的相关知识点,需要掌握所要考察的全体对象叫总体,组成总体的每一个考察对象叫个体,被抽取的那部分个体组成总体的一个样本,样本中个体的数目叫这个样本的容量(样本容量没有单位);特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图)才能正确解答此题.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案【题目】某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20m3时,按2元/m3计算;月用水量超过20m3时,其中的20m3仍按2元/m3计算,超过部分按2.6元/m3计算.设某户家庭月用水量xm3.
月份 | 4月 | 5月 | 6月 |
用水量 | 15 | 17 | 21 |
(1)用含x的式子表示:
当0≤x≤20时,水费为 元;
当x>20时,水费为 元.
(2)小花家第二季度用水情况如上表,小花家这个季度共缴纳水费多少元?