题目内容
如图,平面直角坐标系中,直线AB解析式为:y=-
| ||
| 3 |
| 3 |
 于A、B两点.
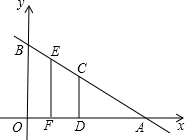
于A、B两点.(1)求A、B两点的坐标;
(2)若点C是AB的中点,过点C作CD⊥x轴于点D,E,F分别为BC,OD的中点,求点E的坐标;
(3)在第一象限内是否存在点P,使得以P,O,B为顶点的三角形与△OBA相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
分析:(1)根据直线解析式与坐标轴的交点求出A、B两点的坐标;
(2)利用:△ACD∽△ABO求出AD、CD,再根据EF是梯形OBCD的中位线求出EF的长进而求出E点坐标;
(3)先确定△OPB的直角所在的定点然后分情况讨论进行分析和排除.
(2)利用:△ACD∽△ABO求出AD、CD,再根据EF是梯形OBCD的中位线求出EF的长进而求出E点坐标;
(3)先确定△OPB的直角所在的定点然后分情况讨论进行分析和排除.
解答:解:(1)将y=0代入y=-
x+
解得x=3,即A点坐标为(3,0)
将x=0代入y=-
x+
解得y=
,即B点坐标为(0,
);
(2)证得:△ACD∽△ABO CD=
BO=
,AD=OD=
AO=
∵E,F分别为BC,OD的中点,CD∥BO
∴EF=
(BO+CD)=
(
+
)=
OF=
OD=
∴E(
,
) …5分
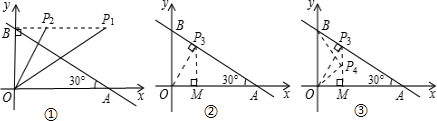
(3)当∠OBP=90°时,如图①若△BOP∽△OBA,则∠BOP=∠BAO=30°,BP=
OB=3,∴P1(3,
).
②若△BPO∽△OBA,则∠BPO=∠BAO=30°,OP=
OB=1.
∴P2(1,
).
当∠OPB=90°时③过点P作OP⊥BC于点P(如图②),此时△PBO∽△OBA,∠BOP=∠BAO=30°
过点P作PM⊥OA于点M.
方法一:在Rt△PBO中,BP=
OB=
,OP=
BP=
.
∵在Rt△PMO中,∠OPM=30°,
∴OM=
OP=
;PM=
OM=
.
∴(
,
).
方法二:设P(x,-
x+
),得OM=x,PM=-
x+
,由∠BOP=∠BAO,得∠POM=∠ABO.
∵tan∠POM=
=tan∠ABO=
=
.
∴-
x+
=
x,解得x=
.此时,(
,
).
④若△POB∽△OBA(如图③),则∠OBP=∠BAO=30°,∠POM=30°.
∴PM=OM=
.
∴P4(
,
)(由对称性也可得到点P4的坐标).
当∠OPB=90°时,点P在x轴上,不符合要求.
综合得,符合条件的点有四个,分别是:P1(3,
),P2(1,
),P3(
,
),P4(
,
). …做出一种情况1分
| ||
| 3 |
| 3 |
将x=0代入y=-
| ||
| 3 |
| 3 |
| 3 |
| 3 |
(2)证得:△ACD∽△ABO CD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
∵E,F分别为BC,OD的中点,CD∥BO
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
∴E(
| 3 |
| 4 |
| ||
| 4 |
(3)当∠OBP=90°时,如图①若△BOP∽△OBA,则∠BOP=∠BAO=30°,BP=
| 3 |
| ||
| 3 |

②若△BPO∽△OBA,则∠BPO=∠BAO=30°,OP=
| ||
| 3 |
∴P2(1,
| 3 |
当∠OPB=90°时③过点P作OP⊥BC于点P(如图②),此时△PBO∽△OBA,∠BOP=∠BAO=30°
过点P作PM⊥OA于点M.
方法一:在Rt△PBO中,BP=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |
∵在Rt△PMO中,∠OPM=30°,
∴OM=
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
3
| ||
| 4 |
∴(
| 3 |
| 4 |
3
| ||
| 4 |
方法二:设P(x,-
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |
∵tan∠POM=
| PM |
| OM |
| OA |
| OB |
| 3 |
∴-
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
3
| ||
| 4 |
④若△POB∽△OBA(如图③),则∠OBP=∠BAO=30°,∠POM=30°.
∴PM=OM=
| ||
| 4 |
∴P4(
| 3 |
| 4 |
| ||
| 4 |
当∠OPB=90°时,点P在x轴上,不符合要求.
综合得,符合条件的点有四个,分别是:P1(3,
| ||
| 3 |
| 3 |
| 3 |
| 4 |
3
| ||
| 4 |
| 3 |
| 4 |
| ||
| 4 |
点评:本题重点考查了一次函数和相似三角形性质相结合的问题,是典型的数形结合的题目.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
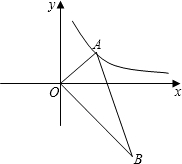 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线 =2
=2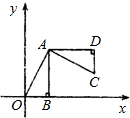 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
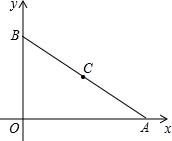 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.