Question

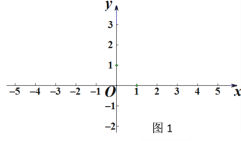
【题目】（1）尺规作图：如图1，请在x轴上作出表示（，0）的点（保留清晰作图痕迹，不写作法）．

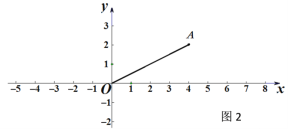
（2）如图2，已知点A（4，2），点B在x轴上，若∠OAB=90°，试求点B的坐标；

（3）如图3，已知点A（4，2），点C在x轴上，若△OAC为等腰三角形，试求点C的坐标．

Answer 1

【答案】（1）答案见解析；（2）（5，0）；（3）（8，0），（2.5，0），（，0），（-，0）．

【解析】

（1）过2作y轴的垂线，过－4作x轴的垂线，交于点B，连接OB，以O为圆心，OB为半径作弧交x轴负半轴于点A，则点A就是所求的点．

（2）用待定系数法求出直线OA的解析式．设直线AB为y=ax+b，由BA⊥OA，得到a=－2，把A（4，2）代入得到b的值，从而得到直线AB的解析式，令y=0，求得x的值，即可得到结论．

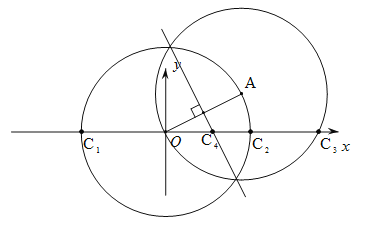
（3）分三种情况讨论：①以O为圆心，OA为半径作圆O交x轴于点C1，C2；②以A为圆心，OA为半径作圆A交x轴于点O，C3；③作OA的垂直平分线交x轴于点C4．分别求出点C的坐标即可．

（1）如图，过2作y轴的垂线，过－4作x轴的垂线，交于点B，连接OB，以O为圆心，OB为半径作弧交x轴负半轴于点A，则OA=OB=，∴A（，0）．

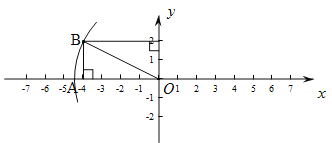
（2）设直线OA为y=kx，把A（4，2）代入得：2=4k，解得：k=，∴直线OA的解析式为y=x．设直线AB为y=ax+b．

∵BA⊥OA，则a=－2，∴直线AB为y=－2x+b，把A（4，2）代入得：2=－2×4+b，解得：b=10，∴y=－2x+10．在y=－2x+10中，令y=0，解得：x=5，∴B（5，0）．

（3）分三种情况讨论：

①以O为圆心，OA为半径作圆O交x轴于点C1，C2，则OC1=OC2=OA=，∴C1（，0），C2（，0）；

②以A为圆心，OA为半径作圆A交x轴于点O，C3，则OC3=2×4=8，∴C3（8，0）；

③作OA的垂直平分线交x轴于点C4，则OC4=AC4．设C4（x，0），则 ，解得：x=2.5，∴C4（2.5，0）．

综上所述：点C的坐标为（8，0）或（2.5，0）或（，0）或（-，0）．