题目内容
【题目】已知关于x的一元二次方程
求证：无论m取何值，方程总有两个不相等的实数根；
若a和b是这个一元二次方程的两个根，求
的最小值．
【答案】（1）证明见解析；（2）3.
【解析】
（1）根据方程的系数结合根的判别式，可得出△=m2+4＞0，从而证出无论m取何值，原方程总有两个不相等的实数根；
（2）由根与系数的关系可得出a+b=﹣[﹣（m+2）]，ab=m，结合a2+b2=（a+b）2﹣2ab解答．
（1）在关于x的一元二次方程x2﹣（m+2）x+m=0中a=1，b=﹣（m+2），c=m，
所以△=m2+4m+4﹣4m=m2+4，
无论m取何值，m2+4＞0，
所以，无论m取何值，方程总有两个不相等的实数根；
（2）因为a和b是这个一元二次方程的两个根，
所以a+b=﹣[﹣（m+2）]=m+2，ab=m，
所以a2+b2=（a+b）2﹣2ab=（m+2）2﹣2m=m2+2m+4=（m+1）2+3．
无论m为何值，（m+1）2≥0，所以a2+b2的最小值为3．
名校练考卷期末冲刺卷系列答案【题目】甲、乙两校的学生人数基本相同，为了解这两所学校学生的数学学业水平，在同一次测试中，从两校各随机抽取了30名学生的测试成绩进行调查分析，其中甲校已经绘制好了条形统计图，乙校只完成了一部分．
甲校 93 82 76 77 76 89 89 89 83 87 88 89 84 92 87
89 79 54 88 92 90 87 68 76 94 84 76 69 83 92
乙校 84 63 90 89 71 92 87 92 85 61 79 91 84 92 92
73 76 92 84 57 87 89 88 94 83 85 80 94 72 90
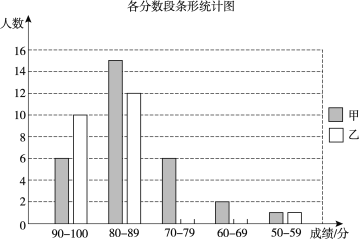
（1）请根据乙校的数据补全条形统计图；
（2）两组样本数据的平均数、中位数、众数如下表所示，请补全表格；
平均数 | 中位数 | 众数 | |
甲校 | 83.4 | 87 | 89 |
乙校 | 83.2 |
（3）两所学校的同学都想依据抽样的数据说明自己学校学生的数学学业水平更好一些，
请为他们各写出一条可以使用的理由；
甲校： ．乙校： ．
（4）综合来看，可以推断出 校学生的数学学业水平更好一些，理由为 ．
