Question

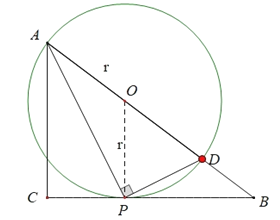
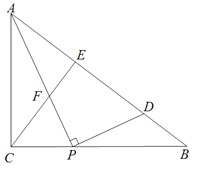
【题目】如图，已知△ABC中，∠ACB=90°，AC=15，BC=20．动点P在线段CB上，以1cm/s的速度从点C向B运动，连接AP，作CE⊥AB分别交AP、AB于点F、E，过点P作PD⊥AP交AB于点D．

（1）线段CE= ；

（2）若t=5时，求证：△BPD≌△ACF；

（3）t为何值时，△PDB是等腰三角形；

（4）求D点经过的路径长．

Answer 1

【答案】（1）12；（2）答案见解析；（3）；（4）12.5

【解析】试题分析：（1）由勾股定理求出AB的长，再由面积法即可得到结论；

（2）用ASA证明即可；

（3）作DG⊥BC，垂足为G，由（2）得∠CAP=∠GPD，可得△ACP∽△PGD．分三种情况讨论：①DP=DB，②PD=PB，③PB=DB；

（4）当AP平分∠CAB时，D′B最长，点CB上运动时，D在D′B之间往返运动．故点D运动路径的长=2BD′，求出BD′的长即可．

试题解析：解：（1）∵∠ACB=90°，AC=15，BC=20，∴AB==25．∵ABCE=ACBC，，∴25CE=15×20，解得：CE=12．

（2）∵ t=5，∴BF=15，∴AC=BF

∵∠APC+∠BPD=∠APC+∠CAP=90° ，∴∠BPD=∠CAP．

∵∠ACE+∠BCE=∠BCE+∠B=90° ，∴∠ACE=∠B，∴△BPD≌△ACF．

（3）作DG⊥BC，垂足为G，由（2）得：∠CAP=∠GPD．∵∠ACP=∠PGD=90°，∴△ACP∽△PGD．分三种情况讨论：

①若DP=DB，则∠GPD=∠B ∴tan∠GPD=tan∠B=，∴ ，∴；

②若PD=PB，则∠PDB=∠B．∵△ACP∽△PGD，∴∠APC=∠PDG．∵∠PDC＞∠B，∴∠PDG＞∠B=∠PDB，则点G在PB的延长线上，矛盾，故PD=PB不成立；

③若PB=DB，则BD=20－t．∵DG∥AC，∴DG：DB=AC：AB，GB：DB=CB：AB，∴DG：(20-t)=15：25，GB：(20-t)=20：25，解得：DG=，GB=，∴PG=PB－GB=(20-t)- =．∵△ACP∽△PGD，∴AC：CP=PG：DG，∴15：t=：，解得：t=45＞20，故PB=DB不成立．

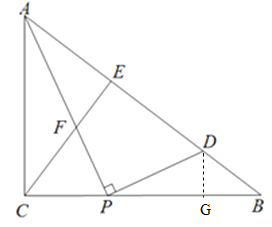
综上所述：t=．

（4）方法一：当AP平分∠CAB时，D′B最长，点CB上运动时，D在D′B之间往返运动．故点D运动路径的长=2BD′．

∵AP平分∠CAB，∴AC：CP=AB：PB，∴15：CP=25：(20-CP)，解得：CP=7.5．∵DG∥AC，∴，设DG=3x，则BG=4x，BD=5x．∵△D′PG∽△PAG，∴D′G：PG=CP：AC=1：2，∴PG=6x，∴6x+4x=PB=20－7.5，解得：x=1.25．∴2 BD′=2×1.25×5=12.5．

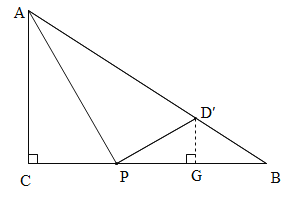
方法二：P点是在CB上运动的，而∠APD是直角，∴P可以看作是斜边AB上以AD为直径的圆O与线段CB的交点，当CB与⊙O相切的时候，此时的D是运动到最远的时候．设半径为OA=OP=r，则OB=25－r．∵OP∥AC，∴OP：AC=OB：AB，∴，r=，∴BD=25－=，∴运动路程为2BD==12.5．