题目内容
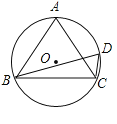
【题目】已知△ABC中,∠A=60°,BC=6.
(1)用尺规作△ABC的外接圆
(2)求∠BOC的度数
(3)求圆O的半径

【答案】(1)作图见解析;(2)∠BOC=120°;(3)![]()
【解析】
(1)画出边AC,AB的垂直平分线,两线交于一点O,以O为圆心,OB长为半径画圆即可;
(2)由圆周角定理即可求出∠BOC的度数;
(3)过点O作OD⊥BC于点D,即可得出CD的长以及∠COD的度数,进而利用锐角三角函数关系求出即可.
(1)如图所示:⊙O即为所求△ABC的外接圆;
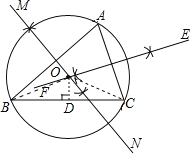
(2)∵∠A=60°,
∴∠BOC=2∠A=120°;
(3)过点O作OD⊥BC于点D,
∵∠A=60°,BC=6,
∴∠COD=60°,CD=![]() BC=3,
BC=3,
∴sin∠COD=![]() ,
,
∴OC=![]() .
.
即⊙O的半径为2![]() .
.

练习册系列答案
相关题目