题目内容
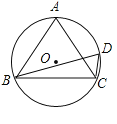
【题目】如图,在圆O中,∠ACB=∠BDC=60°,
(1)求∠BAC的度数;
(2)连接AD,求证:DB=AD+DC.
【答案】(1)60°;(2)证明见解析.
【解析】
(1)根据∠BAC与∠BDC是同弧所对的圆周角即可解答;
(2)连接AD并延长至F,使DE=CD,由圆周角定理及平角的性质可得出△CDE是等边三角形,再由ASA定理可得△DBC≌△CAE,由全等三角形的性质即可得出结论.
(1)∵∠BAC与∠BDC是![]() 所对的圆周角,∠BDC=60°,
所对的圆周角,∠BDC=60°,
∴∠BAC=60°.
(2)连接AD并延长至E,使DE=CD,连接CE,
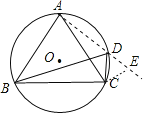
∵∠ACB=∠BDC=60°,
∴∠ADB=∠BDC=60°,
∴∠CDE=180°-∠ADB-∠BDC=180°-60°-60°=60°,
∴△CDE是等边三角形,∠DCE=60°,
∴∠BCA+∠ACD=∠DCE+∠ACD,
∴∠BCD=∠ACE,
∵∠DAC与∠DBC是同弧所对的圆周角,
∴∠DAC=∠DBC,
∵△ABC是等边三角形,
∴BC=AC,
∴△DBC≌△CAE,
∴BD=AE,即DB=DA+DC.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案【题目】近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 ,该中位数的意义是 ;
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
【题目】某厂按用户的月需求量![]() (件)完成一种产品的生产,其中
(件)完成一种产品的生产,其中![]() .每件的售价为18万元,每件的成本
.每件的售价为18万元,每件的成本![]() (万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量
(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量![]() (件)成反比.经市场调研发现,月需求量
(件)成反比.经市场调研发现,月需求量![]() 与月份
与月份![]() (
(![]() 为整数,
为整数,![]() )符合关系式
)符合关系式![]() (
(![]() 为常数),且得到了表中的数据.
为常数),且得到了表中的数据.
月份 | 1 | 2 |
成本 | 11 | 12 |
需求量 | 120 | 100 |
(1)求![]() 与
与![]() 满足的关系式,请说明一件产品的利润能否是12万元;
满足的关系式,请说明一件产品的利润能否是12万元;
(2)求![]() ,并推断是否存在某个月既无盈利也不亏损;
,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第![]() 个月和第
个月和第![]() 个月的利润相差最大,求
个月的利润相差最大,求![]() .
.