��Ŀ����
����Ŀ�����������ǵĺ͵���90�㣬��ô���Ǿͳ��������ǻ�Ϊ��ǣ����ƿ��Զ��壺��������ǵIJ�ľ���ֵ����90�㣬��ô���ǾͿ��Գ��������ǻ�Ϊ���ǣ����磺��1��120�㣬��2��30�㣬|��1����2|��90�㣬���1�͡�2��Ϊ����(���������нǶ���ָ����0����С��180���Ľ�)��
(1)��ͼ��OΪֱ��AB��һ����OC��AB�ڵ�O��OE��OD�ڵ�O ����д��ͼ�����л�Ϊ���ǵĽǣ�_______________________________________________________��
(2)���һ���ǵĴ��ǵ�������ǵIJ��ǵ�![]() ��������ǵĶ�����
��������ǵĶ�����
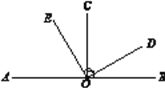
���𰸡� (1) ��EOB���DOB����EOB���EOC����AOD���COD����AOD���AOE
(2) ����ǵĶ���Ϊ30����130��
��������
(1)���ݻ�Ϊ���Ƕ��弴�����;(2) �������Ϊx,����һ���ǵĴ��ǵ�������ǵIJ��ǵ�![]() ���з��̼������.
���з��̼������.
(1) ���ݻ�Ϊ���Ƕ���ɵã���EOB���DOB����EOB���EOC����AOD���COD����AOD���AOE
(2)������ǵĶ���Ϊx����
�ٵ�0��<x<90��ʱ�����Ĵ�����90�㣫x��
�������У�90�㣫x��![]() (180�㣭x)��
(180�㣭x)��
���x��30��.
�ڵ�90��<x<180��ʱ�����Ĵ�����x��90�㣬
�������У�x��90�㣽![]() (180�㣭x)��
(180�㣭x)��
���x��130��.
������ǵĶ���Ϊ30���130��.

 ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�����Ŀ���±���¼��һ����Ա�ڷ�������Ͷ���Ľ����
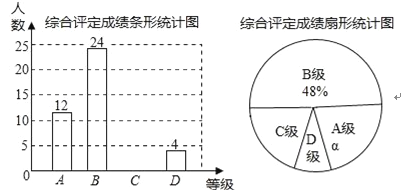
Ͷ��������n�� | 50 | 100 | 150 | 209 | 250 | 300 | 350 |
Ͷ�д�����m�� | 28 | 60 | 78 | 104 | 123 | 152 | 175 |
Ͷ��Ƶ�ʣ�n/m�� | 0.56 | 0.60 | �� | 0.49 | �� | �� |
��1�����㲢��д���е�Ͷ��Ƶ�ʣ���ȷ��0.01����
��2��������ԱͶ��һ�Σ�Ͷ�еĸ���Լ�Ƕ��٣���ȷ��0.1����
����Ŀ��.ij����ʵʩ������ˮ�����ǰ���Ծ���������ˮ��������˵��飬�±���ͨ�������������õ�50����ͥȥ����ƽ����ˮ��![]() ��λ����
��λ����![]() �������������ݽ�������������
�������������ݽ�������������

Ƶ���ֲ���
���� | ���� | Ƶ�� |
| ���� | 11 |
|
| 19 |
| ||
�ϼ� |
| 2 50 |
![]() ������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ����������
������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ����������
![]() ��ֱ��ͼ�����ܵõ�ʲô��Ϣ��
��ֱ��ͼ�����ܵõ�ʲô��Ϣ�� ![]() д����������
���������![]() ��
��
![]() Ϊ�˹�����Լ��ˮ��Ҫȷ��һ����ˮ���ı�������������IJ��ְ�
Ϊ�˹�����Լ��ˮ��Ҫȷ��һ����ˮ���ı�������������IJ��ְ�![]() ���۸��շѣ���Ҫʹ
���۸��շѣ���Ҫʹ![]() �ļ�ͥ�շѲ���Ӱ�죬����ü�ͥ�¾���ˮ��Ӧ�ö�Ϊ���٣�Ϊʲô��
�ļ�ͥ�շѲ���Ӱ�죬����ü�ͥ�¾���ˮ��Ӧ�ö�Ϊ���٣�Ϊʲô��