Question

【题目】如图，直线y=k1x+7（k1＜0）与x轴交于点A，与y轴交于点B，与反比例函数y= （k2＞0）的图象在第一象限交于C、D两点，点O为坐标原点，△AOB的面积为 ，点C横坐标为1．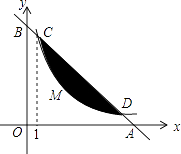
（1）求反比例函数的解析式；
（2）如果一个点的横、纵坐标都是整数，那么我们就称这个点为“整点”，请求出图中阴影部分（不含边界）所包含的所有整点的坐标．

Answer 1

【答案】
（1）解：∵当x=0时，y=7，当y=0时，x=﹣ ，

∴A（﹣ ，0）、B（0、7）．

∴S△AOB= |OA||OB|= ×（﹣ ）×7= ，解得k1=﹣1．

∴直线的解析式为y=﹣x+7．

∵当x=1时，y=﹣1+7=6，

∴C（1，6）．

∴k2=1×6=6．

∴反比例函数的解析式为y=

（2）解：∵点C与点D关于y=x对称，

∴D（6，1）．

当x=2时，反比例函数图象上的点为（2，3），直线上的点为（2，5），此时可得整点为（2，4）；

当x=3时，反比例函数图象上的点为（3，2），直线上的点为（3，4），此时可得整点为（3，3）；

当x=4时，反比例函数图象上的点为（4， ），直线上的点为（4，3），此时可得整点为（4，2）；

当x=5时，反比例函数图象上的点为（5， ），直线上的点为（5，2），此时，不存在整点．

综上所述，符合条件的整点有（2，4）、（3，3）、（4，2）

【解析】（1）分别令x=0、y=0，求得对应y和x的值，从而的得到点A、B的坐标，然后依据三角形的面积公式可求得k1的值，然后由直线的解析式可求得点C的坐标，由点C的坐标可求得反比例函数的解析式；（2）由函数的对称性可求得D（6，1），从而可求得x的值范围，然后求得当x=2、3、4、5时，一次函数和反比例函数对应的函数值，从而可得到整点的坐标．