题目内容
【题目】已知,四边形ABCD是正方形,点P在直线BC上,点G在直线AD上(P、G不与正方形顶点重合,且在CD的同侧),PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连结EF.
(1)如图1,当点P与点G分别在线段BC与线段AD上时.
①求证:DG=2PC;
②求证:四边形PEFD是菱形;
(2)如图2,当点P与点G分别在线段BC与线段AD的延长线上时,请猜想四边形PEFD是怎样的特殊四边形,并证明你的猜想.

【答案】(1)①证明见解析;②证明见解析;(2)四边形PEFD是菱形.理由见解析.
【解析】试题分析:(1)①作PM⊥DG于M,根据等腰三角形的性质由PD=PG得MG=MD,根据矩形的判定易得四边形PCDM为矩形,则PC=MD,于是有DG=2PC;
②根据四边形ABCD为正方形得AD=AB,由四边形ABPM为矩形得AB=PM,则AD=PM,再利用等角的余角相等得到∠GDH=∠MPG,于是可根据“ASA”证明△ADF≌△MPG,得到DF=PG,加上PD=PG,得到DF=PD,然后利用旋转的性质得∠EPG=90°,PE=PG,所以PE=PD=DF,再利用DF⊥PG得到DF∥PE,于是可判断四边形PEFD为平行四边形,加上DF=PD,则可判断四边形PEFD为菱形;
(2)与(1)中②的证明方法一样可得到四边形PEFD为菱形.
试题解析:(1)①作PM⊥DG于M,如图1,

∵PD=PG,
∴MG=MD,
∵四边形ABCD为矩形,
∴PCDM为矩形,
∴PC=MD,
∴DG=2PC;
②∵四边形ABCD为正方形,
∴AD=AB,
∵四边形ABPM为矩形,
∴AB=PM,
∴AD=PM,
∵DF⊥PG,
∴∠DHG=90°,
∴∠GDH+∠DGH=90°,
∵∠MGP+∠MPG=90°,
∴∠GDH=∠MPG,
在△ADF和△MPG中, 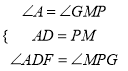 ,
,
∴△ADF≌△MPG(ASA),
∴DF=PG,
而PD=PG,
∴DF=PD,
∵线段PG绕点P逆时针旋转90°得到线段PE,
∴∠EPG=90°,PE=PG,
∴PE=PD=DF,
而DF⊥PG,
∴DF∥PE,
即DF∥PE,且DF=PE,
∴四边形PEFD为平行四边形,
∵DF=PD,
∴四边形PEFD为菱形;
(2)解:四边形PEFD是菱形.理由如下:
作PM⊥DG于M,如图2,

与(1)一样同理可证得△ADF≌△MPG,
∴DF=PG,
而PD=PG,
∴DF=PD,
∵线段PG绕点P逆时针旋转90°得到线段PE,
∴∠EPG=90°,PE=PG,
∴PE=PD=DF
而DF⊥PG,
∴DF∥PE,
即DF∥PE,且DF=PE,
∴四边形PEFD为平行四边形,
∵DF=PD,
∴四边形PEFD为菱形.







