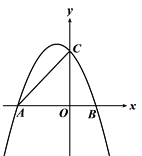��Ŀ����
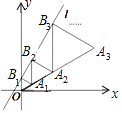
����Ŀ��С����ѧϰ������������ͼ��ʱ��������ʦҪ��ͬѧ�Ǹ�����̽��һ�κ���y1=x+1��ͼ�����Ļ������裬��ֽ����̽������y2=![]() ��ͼ�����ںڰ���д��4��������꣺A��
��ͼ�����ںڰ���д��4��������꣺A��![]() ��
��![]() ����B��1��2����C��1��
����B��1��2����C��1��![]() ����D����2����1����
����D����2����1����
��1����A��B��C��D�ĸ����У���ȡһ���㣬��������ֱ��y1=x+1����˫����y2=![]() �ϵĸ����Ƕ��٣�
�ϵĸ����Ƕ��٣�
��2��С����A��B��C��D�ĸ�������ȡ�����������㣬�����㶼����˫����y2=![]() �ϵĸ��ʣ�
�ϵĸ��ʣ�
���𰸡���1��![]() ����2��
����2��![]() ��
��
��������
���⣨1�����ĸ��� ������ֱ����һ�κ����ͷ����������Ľ���ʽ��֪��B���D����ֱ��y=x+1�ϣ�����˫����y=![]() �ϣ��ݴ˼��������ȡһ���㣬��������ֱ��y1=x+1����˫����y2=
�ϣ��ݴ˼��������ȡһ���㣬��������ֱ��y1=x+1����˫����y2=![]() �ϵĸ��ʣ�
�ϵĸ��ʣ�
��2����A��B��C��D�ĸ�����������ѡ�����������㣬��6�ֵȿ��ܵ�������ֱ��ǣ�AB��AC��AD��BC��BD��CD�����У������㶼����˫����![]() ������AB��AD��BD ����������Ӷ�������㶼����˫����
������AB��AD��BD ����������Ӷ�������㶼����˫����![]() �ĸ��ʣ�
�ĸ��ʣ�
�����������1����A��B��C��D�ֱ����y1=x+1�ͺ���y2=![]() ��֪����B���D����ֱ��y=x+1�ϣ�����˫����y=
��֪����B���D����ֱ��y=x+1�ϣ�����˫����y=![]() �ϣ�
�ϣ�
�����ȡһ���㣬����ֱ������˫�����ϵĸ�����![]() ��
��
��2���ɣ�1���ɵã�����A��B��C��D�ĸ�����������ѡ��������������
��6�ֵȿ��ܵ�������ֱ��ǣ�AB��AC��AD��BC��BD��CD��
���У������㶼����˫����![]() ������AB��AD��BD ���������
������AB��AD��BD ���������
�����㶼����˫����![]() �ĸ����ǣ�
�ĸ����ǣ�![]()
![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�