题目内容
【题目】如图，在△ABC中，∠A=90°，AB=2cm，AC=4cm．动点P从点A出发，沿AB方向以1cm/s的速度向点B运动，动点Q从点B同时出发，沿BA方向以1cm/s的速度向点A运动．当点P到达点B时，P，Q两点同时停止运动，以AP为一边向上作正方形APDE，过点Q作QF∥BC，交AC于点F．设点P的运动时间为ts，正方形和梯形重合部分的面积为Scm2．
（1）当t= _________ s时，点P与点Q重合；
（2）当t= _________ s时，点D在QF上；
（3）当点P在Q，B两点之间（不包括Q，B两点）时，求S与t之间的函数关系式．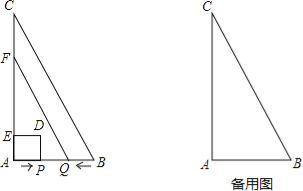
【答案】（1）1 （2）
（3）
【解析】
试题（1）当点P与点Q重合时，AP=BQ=t，且AP+BQ=AB=2，
∴t+t=2，解得t=1s，
故填空答案：1．
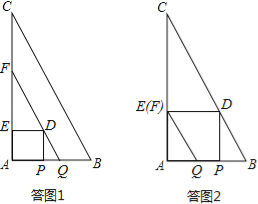
（2）当点D在QF上时，如答图1所示，此时AP=BQ=t．
∵QF∥BC，APDE为正方形，∴△PQD∽△ABC，
∴DP：PQ=AC：AB=2，则PQ=
DP=AP=t．
由AP+PQ+BQ=AB=2，得t+t+t=2，解得：t=
．
故填空答案：．
（3）当P、Q重合时，由（1）知，此时t=1；
当D点在BC上时，如答图2所示，此时AP=BQ=t，BP=
t，求得t=
s，进一步分析可知此时点E与点F重合；
当点P到达B点时，此时t=2．
因此当P点在Q，B两点之间（不包括Q，B两点）时，其运动过程可分析如下：
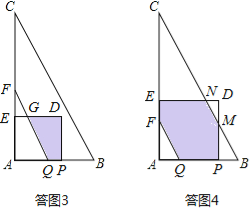
①当1＜t≤时，如答图3所示，此时重合部分为梯形PDGQ．
此时AP=BQ=t，∴AQ=2﹣t，PQ=AP﹣AQ=2t﹣2；
易知△ABC∽△AQF，可得AF=2AQ，EF=2EG．
∴EF=AF﹣AE=2（2﹣t）﹣t=4﹣3t，EG=EF=2﹣
t，
∴DG=DE﹣EG=t﹣（2﹣t）=
t﹣2．
S=S梯形PDGQ=
（PQ+DG）PD=[（2t﹣2）+（t﹣2）]t=
t2﹣2t；
②当
＜t＜2时，如答图4所示，此时重合部分为一个多边形．
此时AP=BQ=t，∴AQ=PB=2﹣t，
易知△ABC∽△AQF∽△PBM∽△DNM，可得AF=2AQ，PM=2PB，DM=2DN，
∴AF=4﹣2t，PM=4﹣2t．
又DM=DP﹣PM=t﹣（4﹣2t）=3t﹣4，∴DN=（3t﹣4）．
S=S正方形APDE﹣S△AQF﹣S△DMN=AP2﹣AQAF﹣
DNDM
=t2﹣（2﹣t）（4﹣2t）﹣×（3t﹣4）×（3t﹣4）
=﹣
t2+10t﹣8．
综上所述，当点P在Q，B两点之间（不包括Q，B两点）时，S与t之间的函数关系式为：
S=．
