Question

【题目】如图是某货站传送货物的平面示意图．为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°．已知原传送带AB长为4米．

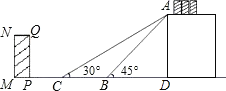
（1）求新传送带AC的长度．

（2）如果需要在货物着地点C的左侧留出2米的通道，试判断距离B点5米的货物MNQP是否需要挪走，并说明理由．

参考数据：．

Answer 1

【答案】（1）AC的长度约为8米；（2）货物MNQP不应挪走．

【解析】

试题分析：（1）在构建的直角三角形中，首先求出两个直角三角形的公共直角边，进而在Rt△ACD中，求出AC的长．

（2）通过解直角三角形，可求出BD、CD的长，进而可求出BC、PC的长．然后判断PC的值是否大于2米即可．

解：（1）如图，

在Rt△ABD中，AD=ABsin45°=4×=4．

在Rt△ACD中，

∵∠ACD=30°，

∴AC=2AD=8．

即新传送带AC的长度约为8米；

（2）结论：货物MNQP不用挪走． （5分）

解：在Rt△ABD中，BD=ABcos45°=4×=4．

在Rt△ACD中，CD=ACcos30°=2．

∴CB=CD﹣BD=2﹣4≈0.9．

∵PC=PB﹣CB≈4﹣0.9=3.1＞2，

∴货物MNQP不应挪走．