题目内容
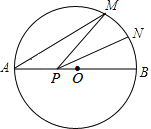
【题目】如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点.若MN=1,则△PMN周长的最小值为( )
A.4 B.5 C.6 D.7
【答案】B
【解析】
试题分析:作N关于AB的对称点N′,连接MN′,NN′,ON′,ON,由两点之间线段最短可知MN′与AB的交点P′即为△PMN周长的最小时的点,根据N是弧MB的中点可知∠A=∠NOB=∠MON=20°,故可得出∠MON′=60°,故△MON′为等边三角形,由此可得出结论.
解:作N关于AB的对称点N′,连接MN′,NN′,ON′,ON.
∵N关于AB的对称点N′,
∴MN′与AB的交点P′即为△PMN周长的最小时的点,
∵N是弧MB的中点,
∴∠A=∠NOB=∠MON=20°,
∴∠MON′=60°,
∴△MON′为等边三角形,
∴MN′=OM=4,
∴△PMN周长的最小值为4+1=5.
故选:B.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目