题目内容
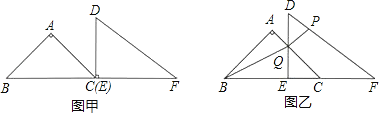
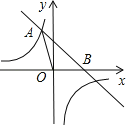
【题目】如图，直角三角板ABC的斜边AB=12cm，∠A=30°，将三角板ABC绕C顺时针旋转90°至三角板A'B'C'的位置后，再沿CB方向向左平移，使点B'落在原三角板ABC的斜边AB上，则三角板A'B'C'平移的距离为（ ）
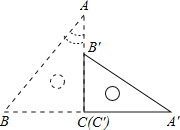
A．6cm B．4cm C．（6﹣
）cm D．（
）cm
【答案】C
【解析】
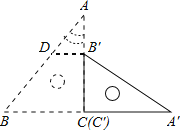
试题分析：如图，过B′作B′D⊥AC，垂足为B′，则三角板A'B'C'平移的距离为B′D的长，根据AB′=AC﹣B′C，∠A=30°，在Rt△AB′D中，解直角三角形求B′D即可．
解：如图，过B′作B′D⊥AC，垂足为B′，
∵在Rt△ABC中，AB=12，∠A=30°，
∴BC=
AB=6，AC=ABcos30°=6
，
由旋转的性质可知B′C=BC=6，
∴AB′=AC﹣B′C=6﹣6，
在Rt△AB′D中，∵∠A=30°，
∴B′D=AB′tan30°=（6﹣6）×
=（6﹣2）cm．
故选C．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
