题目内容
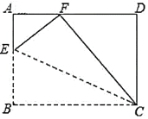
【题目】如图,在矩形![]() 中,
中,![]() =3,
=3,![]() =5,
=5,![]() 是
是![]() 上一点,连结
上一点,连结![]() ,将
,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 的对应点
的对应点![]() 落在边
落在边![]() 上,则△
上,则△![]() 的面积为__________.
的面积为__________.
【答案】![]()
【解析】
根据矩形的性质得到∠A=∠B=∠D=90°,CD=AB=3,BC=AD=5,根据折叠的性质得到CF=CB=5,EF=BE,根据勾股定理得到DF=![]() =4,AE=
=4,AE=![]() ,于是得到结论.
,于是得到结论.
∵在矩形ABCD中,AB=3,AD=5,
∴∠A=∠B=∠D=90°,CD=AB=3,BC=AD=5,
∵将△BCE沿CE翻折,使点B的对应点F落在边AD上,
∴CF=CB=5,EF=BE,
∴DF=![]() =4,
=4,
∴AF=AD﹣DF=5﹣4=1,
∵EF2=AE2+AF2,
∴(3﹣AE)2=AE2+12,
解得:AE=![]() ,
,
∴△AEF的面积=![]() AEAF=
AEAF=![]() ×1=
×1=![]()
故答案为:![]() .
.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目