题目内容
【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
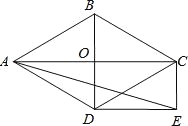
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2![]() 时,求sin∠AED的值,求∠EAD的正切值.
时,求sin∠AED的值,求∠EAD的正切值.
【答案】(1)证明见解析(2)![]()
【解析】
试题分析:(1)先证四边形ODEC是平行四边形,然后根据菱形的对角线互相垂直,得到∠DOC=90°,根据矩形的定义即可判定四边形ODEC是矩形;
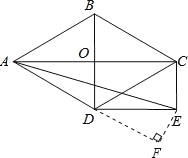
(2)如图,过点E作EF⊥AD,交AD的延长线于F,构建直角△DEF,在该直角三角形中,∠F=90°,∠EDF=30°,易求DF的长度.所以通过解Rt△AFE来求tan∠EAD的值.
试题解析:(1)∵CE∥BD,DE∥AC,
∴四边形ODEC是平行四边形.
又∵菱形ABCD,
∴AC⊥BD,
∴∠DOC=90°.
∴四边形ODEC是矩形.
(2)如图,过点E作EF⊥AD,交AD的延长线于F.
∵AC⊥BD,∠ADB=60°,AD=2![]() ,
,
∴OD=![]() ,AO=OC=3.
,AO=OC=3.
∵四边形ODEC是矩形,
∴DE=OC=3,∠ODE=90°.
又∵∠ADO+∠ODE+∠EDF=180°,
∴∠EDF=30°.
在Rt△DEF中,∠F=90°,∠EDF=30°,
∴EF=![]() DE=
DE=![]() .
.
∴DF=![]() .
.
在Rt△AFE中,∠DFE=90°,
∴tan∠EAD=![]() =
=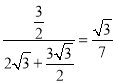 .
.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目