Question

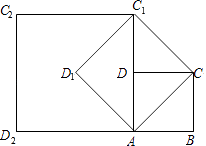
【题目】如图，设正方体ABCD－A1B1C1D1的棱长为1，黑甲壳虫从点A出发，白甲壳虫从点C1出发，它们以相同的速度分别沿棱向前爬行．黑甲壳虫爬行的路线是：AA1→A1D1→D1C1→C1C→CB→BA→AA1→A1D1…，白甲壳虫爬行的路线是：C1C→CB→BB1→B1C1→C1C→CB…，那么当黑、白两个甲壳虫各爬行完第2018条棱分别停止在所到的正方体顶点处时，它们之间的最短路程的平方是(　　)

A. 2 B. 3 C. 4 D. 5

Answer 1

【答案】B

【解析】

黑甲壳虫爬行的路线是:AA1→A1D1→D1C1→C1C→CB→BA→AA1→A1D1…,

白甲壳虫爬行的路线是:C1C→CB→BB1→B1C1→C1C→CB…,两甲壳虫的路线都有周期，求出最后停止的点，根据勾股定理可得即可.

因为黑甲壳虫爬行的路线是:AA1→A1D1→D1C1→C1C→CB→BA→AA1→A1D1…,

白甲壳虫爬行的路线是:C1C→CB→BB1→B1C1→C1C→CB…,

因此可以判断两个甲壳虫爬行一圈黑甲壳虫一圈6条棱, 因为2018÷6=336…2,

白甲壳虫一圈4条棱，2018÷4=504…2,

所以黑甲壳虫爬行完第2018条棱停止的点是D1,白甲壳虫爬行完第2018条棱停止的点是B,

根据勾股定理可得: BD12=.

故选B.