Question

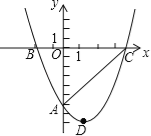
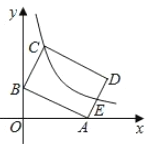
【题目】如图，在平面直角坐标系中，点，，反比例函数的图象经过矩形的顶点，且交边于点，若为的中点，则的值为__________．

Answer 1

【答案】14

【解析】

设法表示点C、E的坐标，通过辅助线，构造相似三角形，设合适未知数，表示出点C、E的坐标，再依据都在反比例函数的图象上，建立方程解出未知数，确定点的坐标，进而确定k的值．

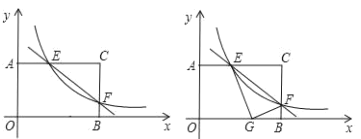
解：过点CE分别作x轴y、轴的垂线，垂足为M、N，如图：

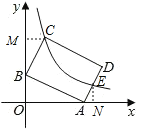
∵ABCD是矩形，

∴∠ABC=∠BAC=90°，

∴∠ABO+∠BAO=∠ABO+∠CBM=90°，

∴∠BAO=∠CBM，

∵∠AOB=∠BMC=90°，

∴△AOB∽△BMC，

∴，

设CM=a，则BM=2a，

∴C（a，2a+3），

同理可得：E（6+a，a）

∵点C、E在反比例函数y=（k＞0）的图象上，

∴a（2a+3）=a（6+a）

∴a1=2，a2=0（舍去），

∴点E的坐标为：（7，2），

∴；

故答案为：14．