题目内容
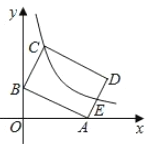
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 中点,点
中点,点![]() 在
在![]() 延长线上,
延长线上,![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
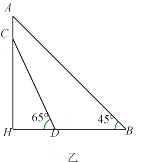
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)求证:![]() ;
;
(3)设![]() 交
交![]() 于点
于点![]() .
.
①若![]() ,
,![]() ,求
,求![]() 的值;
的值;
②连结![]() ,分别记
,分别记![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() ,
,![]() ,当
,当![]() 时,
时,![]() .(直接写出答案)
.(直接写出答案)
【答案】(1)详见解析;(2)详见解析;(3)①![]() ;②
;②![]() .
.
【解析】
(1)根据∠AOB=∠OBC+∠OCB,只要求出∠OBC,∠OCB即可.
(2)想办法证明CG⊥AE即可解决问题.
(3)①如图2中,作MH⊥CE于H,解直角三角形求出AG,GM,ME即可解决问题.
②如图3所示:连接DE.首先证明四边形OCED是平行四边形,再证明EC=2DG,利用平行线分线段成比例定理即可解决问题.
解:(1)∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]() .
.
∴![]() .
.
∴![]() .即
.即![]() .
.
∴![]() .
.
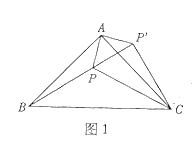
(2)连结![]() (如图1).
(如图1).

∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴四边形![]() 为矩形.
为矩形.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
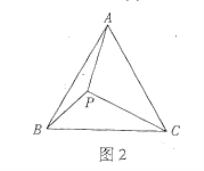
(3)①作![]() 于
于![]() (如图2).
(如图2).

由![]() ,
,![]() ,
,
则四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
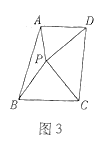
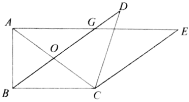
②如图3所示:连接DE.

∵OA=OC,∠ABC=90°,
∴BO=OA=OC,
∴∠OBC=∠OCB,
∵AE∥BC,
∴∠CAE=∠ACB,∠AGO=∠OBC,
∵CA=CE,
∴∠CAE=∠CAE,
∴∠AGB=∠AEC,
∴AD∥CE,
∵DE∥AC,
∴四边形OCED是平行四边形,
∴OD=CE=CA,
∵∠OAG=∠OGA,
∴OA=OG,
∴OA=OC=OG=DG,
∵DG∥EC,
∴![]() ,
,
∴![]() ,
,
设S2=m,则S3=2m,
∴S△DGE=3m,
∵OG=GD,∠AGO=∠DGE,∠OAG=∠DEG,
∴△AGO≌△EGD(AAS),
∴S△AOG=S△DEG=3m,
∵OB=OG,
∴S△ABG=2S△AOG=6m,
∴S1:S2:S3=6m:m:2m=6:1:2.
故答案为:6:1:2.

练习册系列答案
相关题目