题目内容
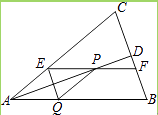
【题目】如图,已知AD∥CB,∠A=∠C,若∠ABD=32°,求∠BDC的度数.有同学用了下面的方法.但由于一时犯急没有写完整,请你帮他添写完整. 解:∵AD∥CB( 已知 )
∴∠C+∠ADC=180° ()
又∵∠A=∠C ()
∴∠A+∠ADC=180° ()
∴AB∥CD ()
∴∠BDC=∠ABD=32° ().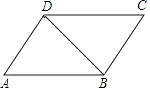
【答案】两直线平行,同旁内角互补;已知;等量代换;同旁内角互补,两直线平行;两直线平行,内错角相等
【解析】解:∵AD∥CB( 已知 ), ∴∠C+∠ADC=180° (两直线平行,同旁内角互补).
又∵∠A=∠C (已知),
∴∠A+∠ADC=180° (等量代换),
∴AB∥CD (同旁内角互补,两直线平行),
∴∠BDC=∠ABD=32° (两直线平行,内错角相等).
所以答案是:两直线平行,同旁内角互补;已知;等量代换;同旁内角互补,两直线平行;两直线平行,内错角相等
【考点精析】根据题目的已知条件,利用平行线的判定与性质的相关知识可以得到问题的答案,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.

练习册系列答案
相关题目