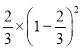��Ŀ����
����Ŀ����ͼ��ֱ��y=��![]() x+c��x�ύ�ڵ�A��3��0������y�ύ�ڵ�B��������y=��
x+c��x�ύ�ڵ�A��3��0������y�ύ�ڵ�B��������y=��![]() x2+bx+c������A��B��
x2+bx+c������A��B��
��1�����B������������ߵĽ���ʽ��
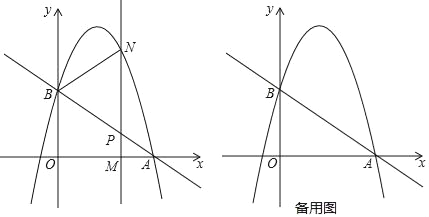
��2��M��m��0��Ϊx����һ���㣬����M�Ҵ�ֱ��x���ֱ����ֱ��AB�������߷ֱ��ڵ�P��N��
�ٵ�M���߶�OA���˶�������B��P��NΪ���������������APM���ƣ����M�����ꣻ
�ڵ�M��x���������˶�����������M��P��N��ǡ��һ�����������������߶ε��е㣨�����غϳ��⣩�����M��P��N����Ϊ����г��������ֱ��д��ʹ��M��P��N�����Ϊ����г������m��ֵ��
���𰸡�(1)�����߽���ʽΪy=��![]() x2+
x2+![]() x+2��(2)�ٵ�M������Ϊ��2.5��0����
x+2��(2)�ٵ�M������Ϊ��2.5��0����![]() ��0������m��ֵΪ
��0������m��ֵΪ![]() ��1��
��1��![]() ��
��
�������������������1����A���������ֱ�߽���ʽ�����c��������B�����꣬��A��B�����꣬���ô���ϵ��������������߽���ʽ��
��2������M������ɱ�ʾP��N�����꣬�Ӷ��ɱ�ʾ��MA��MP��PN��PB�ij�������NBP=90������BNP=90������������ֱ��������������ε����ʿɵõ�����m�ķ��̣������m��ֵ��
����m�ɱ�ʾ��M��P��N�����꣬�������֪��PΪ�߶�MN���е㡢MΪ�߶�PN���е��NΪ�߶�PM���е㣬�ɷֱ�õ�����m�ķ��̣������m��ֵ��
����������⣺
��1����![]() ��x�ύ�ڵ�A��3��0������y�ύ�ڵ�B����0=��2+c�����c=2����B��0��2������������
��x�ύ�ڵ�A��3��0������y�ύ�ڵ�B����0=��2+c�����c=2����B��0��2������������![]() ������A��B����
������A��B����![]() �������
������� 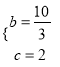 ���������߽���ʽΪ
���������߽���ʽΪ![]() ��
��
��2�����ɣ�1����ֱ֪�߽���ʽΪ![]() ����M��m��0��Ϊx����һ���㣬����M�Ҵ�ֱ��x���ֱ����ֱ��AB�������߷ֱ��ڵ�P��N����P��m��
����M��m��0��Ϊx����һ���㣬����M�Ҵ�ֱ��x���ֱ����ֱ��AB�������߷ֱ��ڵ�P��N����P��m�� ![]() ����N��m��
����N��m�� ![]() ������PM=
������PM=![]() ��PA=3��m��PN=
��PA=3��m��PN=![]() ����
����![]() ��=
��=![]() ���ߡ�BPN����APM���ƣ�����BPN=��APM�����BNP=��AMP=90������NBP=��AMP=90���������������
���ߡ�BPN����APM���ƣ�����BPN=��APM�����BNP=��AMP=90������NBP=��AMP=90���������������
����BNP=90��ʱ������BN��MN�����N��������Ϊ2���� ![]() =2�����m=0����ȥ����m=
=2�����m=0����ȥ����m=![]() ����M��
����M��![]() ��0����
��0����
����NBP=90��ʱ������![]() ����A��3��0����B��0��2����P��m��
����A��3��0����B��0��2����P��m�� ![]() ������BP=
������BP=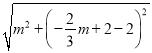 =
= ![]() ��AP=
��AP=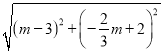 =
=![]() ��3��m������
��3��m������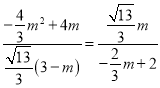 �����m=0����ȥ����m=
�����m=0����ȥ����m=![]() ����M��
����M��![]() ��0����
��0����
���Ͽ�֪����B��P��NΪ���������������APM����ʱ����M������Ϊ��![]() ��0����
��0����![]() ��0����
��0����
��������֪M��m��0����P��m�� ![]() ����N��m��
����N��m�� ![]() ������M��P��N����Ϊ����г����������PΪ�߶�MN���е㡢MΪ�߶�PN���е��NΪ�߶�PM���е㣬��PΪ�߶�MN���е�ʱ������2��
������M��P��N����Ϊ����г����������PΪ�߶�MN���е㡢MΪ�߶�PN���е��NΪ�߶�PM���е㣬��PΪ�߶�MN���е�ʱ������2��![]() ��=
��=![]() �����m=3�������غϣ���ȥ����m=
�����m=3�������غϣ���ȥ����m=![]() ��
��
��MΪ�߶�PN���е�ʱ������![]() +��
+��![]() ��=0�����m=3����ȥ����m=��1��
��=0�����m=3����ȥ����m=��1��
��NΪ�߶�PM���е�ʱ������![]() =2��
=2��![]() �������m=3����ȥ����m=
�������m=3����ȥ����m=![]() ��
��
���Ͽ�֪��M��P��N�����Ϊ����г����ʱm��ֵΪ![]() ��1��
��1��![]() ��
��