题目内容
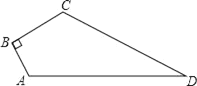
【题目】已知如图,![]() 三点在同一直线上,
三点在同一直线上,![]() .
.
(1)已知点![]() 在直线
在直线![]() 上,根据条件,请补充完整图形,并求
上,根据条件,请补充完整图形,并求![]() 的长;
的长;
![]()
(2)已知点![]() 在直线
在直线![]() 上,
上,![]() 分别是
分别是![]() ,
,![]() 的中点,根据条件,请补充完整图形,并求
的中点,根据条件,请补充完整图形,并求![]() 的长,直接写出
的长,直接写出![]() 与
与![]() 的长存在的数量关系;
的长存在的数量关系;
![]()
(3)已知点![]() 在直线
在直线![]() 上,
上,![]() 分别是
分别是![]() ,
,![]() 的中点,根据条件,请补充完整图形,并求
的中点,根据条件,请补充完整图形,并求![]() 的长,直接写出
的长,直接写出![]() 与
与![]() 的长存在的数量关系.
的长存在的数量关系.
![]()
【答案】(1)图见解析;AC=4或8;(2)图见解析;MN=2或4;MN=![]() ;(3)MN=3;MN=
;(3)MN=3;MN=![]() .
.
【解析】
(1)根据点C的位置有两种情况分类讨论,①当点C在点B的左侧时,易求此时AC的长;②当点C在点B的右侧时,易求此时AC的长;
(2)①当点C在点B的左侧时,根据中点的定义,可得:MB=![]() ,NB=
,NB=![]() ,从而求出MN与AC的长度关系,再根据(1)中此时AC的长,即可求出MN的长;②当点C在点B的右侧时,原理同上;
,从而求出MN与AC的长度关系,再根据(1)中此时AC的长,即可求出MN的长;②当点C在点B的右侧时,原理同上;
(3)①当点C在点B的左侧时,根据中点的定义,可得:MC=![]() ,CN=
,CN=![]() ,从而求出MN与AB的长度关系,即可求出MN;②当点C在点B的右侧时,原理同上.
,从而求出MN与AB的长度关系,即可求出MN;②当点C在点B的右侧时,原理同上.
解:(1)根据题意,点C的位置有两种情况
①当点C在点B的左侧时,补全图形如下所示
![]()
∵![]() ,
,
∴AC=AB-BC=4;
②当点C在点B的右侧时,补全图形如下所示
![]()
∵![]() ,
,
∴AC=AB+BC=8.
综上所述:AC=4或8;
(2)①当点C在点B的左侧时,补全图形如下所示
![]()
∵![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴MB=![]() ,NB=
,NB=![]()
∴MN=MB-NB=![]() -
-![]() ==
==![]() =
=![]()
由(1)可知:此时AC=4
∴MN=![]() =2;
=2;
②当点C在点B的右侧时,补全图形如下所示
![]()
∵![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴MB=![]() ,NB=
,NB=![]()
∴MN=MB+NB=![]() +
+![]() ==
==![]() =
=![]()
由(1)可知:此时AC=8
∴MN=![]() =4;
=4;
综上所述:MN=2或4;MN=![]() ;
;
(3)①当点C在点B的左侧时,补全图形如下所示
![]()
∵![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴MC=![]() ,CN=
,CN=![]()
∴MN=MC+ CN =![]() +
+![]() ==
==![]() =
=![]() =3;
=3;
②当点C在点B的右侧时,补全图形如下所示
![]()
∵![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴MC=![]() ,CN=
,CN=![]()
∴MN=MC- CN =![]() -
-![]() ==
==![]() =
=![]() =3;
=3;
综上所述:MN=3;MN=![]() .
.