题目内容
【题目】如图,在平面直角坐标系xOy中,A是双曲线![]() 在第一象限的分支上的一个动点,连接AO并延长与这个双曲线的另一分支交于点B,以AB为底边作等腰直角三角形ABC,使得点C位于第四象限。
在第一象限的分支上的一个动点,连接AO并延长与这个双曲线的另一分支交于点B,以AB为底边作等腰直角三角形ABC,使得点C位于第四象限。
(1)点C与原点O的最短距离是________;
(2)没点C的坐标为(![]()
![]() ,点A在运动的过程中,y随x的变化而变化,y关于x的函数关系式为________。
,点A在运动的过程中,y随x的变化而变化,y关于x的函数关系式为________。

【答案】![]()
![]()
【解析】
(1)先根据反比例函数的对称性及等腰直角三角形的性质可得OC=OA=OB,利用勾股定理求出AO的长为![]() ,再配方得
,再配方得![]() ,根据非负性即可求出OA的最小值,进而即可求解;
,根据非负性即可求出OA的最小值,进而即可求解;
(2)先证明△AOD≌△COE可得AD=CE,OD=OE,然后根据点C的坐标表示出A的坐标,再由反比例函数的图象与性质即可求出y与x 的函数解析式.
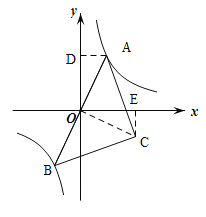
解:(1)连接OC,过点A作AD⊥y轴,如图,
 ,
,
∵A是双曲线![]() 在第一象限的分支上的一个动点,延长AO交另一分支于点B,
在第一象限的分支上的一个动点,延长AO交另一分支于点B,
∴OA=OB,
∵△ABC是等腰直角三角形,
∴OC=OA=OB,
∴当OA的长最短时,OC的长为点C与原点O的最短距离,
设A(m,![]() ),
),
∴AD=m,OD=![]() ,
,
∴OA=![]() =
=![]() =
=![]() ,
,
∵![]() ,
,
∴当![]() 时,OA=
时,OA=![]() 为最小值,
为最小值,
∴点C与原点O的最短距离为![]() .
.
故答案为![]() ;
;
(2)过点C作x轴的垂线,垂足为E,如上图,
∴∠ADO=∠CEO=90°,
∵△ABC是等腰直角三角形,
∴OC=OA=OB,OC⊥AB,
∴∠COE+∠AOE=90°,
∵∠AOD+∠AOE=90°,
∴∠AOD=∠COE,
∴△AOD≌△COE(AAS),
∴AD=CE,OD=OE,
∵点C的坐标为(x,y)(x>0),
∴OE=x,CE=-y,
∴OD=x,AD=-y,
∴点A的坐标为(-y,x),
∵A是双曲线![]() 第一象限的一点,
第一象限的一点,
∴![]() ,即
,即![]() ,
,
∴y关于x的函数关系式为![]() (x>0).
(x>0).
故答案为![]() (x>0).
(x>0).