题目内容
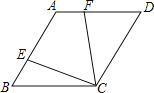
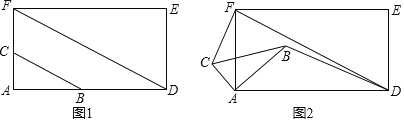
【题目】如图1,Rt△ABC中,∠BAC=90°,四边形ADEF是矩形,点B、C分别在边AD、AF上,且BC∥DF.
(1)求证:![]() ,BD⊥CF;
,BD⊥CF;
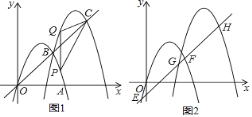
(2)当△ABC绕点A逆时针旋转到图2的位置时,(1)中的结论还成立吗?若成立,请证明,若不成立,请说明理由.
【答案】(1)证明见解析;(2)当△ABC绕点A逆时针旋转到图2的位置时,(1)中的结论还成立.理由见解析.
【解析】
(1)根据平行线分线段成比例即可得出![]() ,然后利用矩形的性质即可证明BD⊥CF;
,然后利用矩形的性质即可证明BD⊥CF;
(2)延长DB交CF于G,交AF于H,先证明△ABC∽△ADF,得出![]() ,再由旋转的性质得出的∠CAF=∠BAD和对应边成比例证明△ABD∽△ACF,根据相似三角形的性质有
,再由旋转的性质得出的∠CAF=∠BAD和对应边成比例证明△ABD∽△ACF,根据相似三角形的性质有![]() ,∠AFC=∠ADB,最后通过等量代换可得到∠FGH=90°,即可证明BD⊥CF.
,∠AFC=∠ADB,最后通过等量代换可得到∠FGH=90°,即可证明BD⊥CF.
(1)∵BC∥DF,
∴![]() ,
,
∵四边形ADEF是矩形,
∴∠A=90°,
∴AD⊥AF,
∴BD⊥CF;
(2)(1)中的结论还成立.理由如下:
延长DB交CF于G,交AF于H,如图2所示:

由(1)得:BC∥DF,
∴∠ABC=∠ADF,∠ACB=∠AFD,
∴△ABC∽△ADF,
∴![]() ,
,
由旋转的性质得∠CAF=∠BAD,
∴△ABD∽△ACF,
∴![]() ,∠AFC=∠ADB.
,∠AFC=∠ADB.
∵∠GHF=∠AHD,∠ADB+∠AHD=90°,
∴∠AFC+∠GHF=90°,
∴∠FGH=90°,
∴BD⊥CF.

练习册系列答案
相关题目