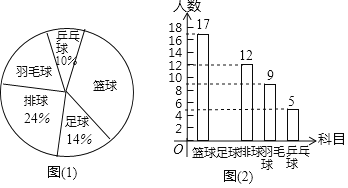
题目内容
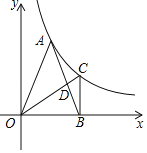
【题目】如图1,抛物线![]() 交
交![]() 正半轴于点
正半轴于点![]() ,将抛物线
,将抛物线![]() 先向右平移3个单位,再向上平移3个单位得到抛物线
先向右平移3个单位,再向上平移3个单位得到抛物线![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .
.
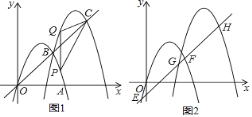
(1)求抛物线![]() 的解析式;
的解析式;
(2)点![]() 是抛物线
是抛物线![]() 上
上![]() 间的一点,作
间的一点,作![]() 轴交抛物线
轴交抛物线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 为何值时,使
为何值时,使![]() 的面积最大,并求出最大值;
的面积最大,并求出最大值;
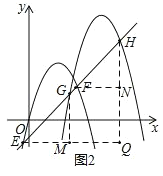
(3)如图2,将直线![]() 向下平移,交抛物线
向下平移,交抛物线![]() 于点
于点![]() ,
,![]() ,交抛物线
,交抛物线![]() 于点
于点![]() ,
,![]() ,则
,则![]() 的值是否为定值,证明你的结论.
的值是否为定值,证明你的结论.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 有最大值,最大值为6;(3)
有最大值,最大值为6;(3)![]() 的值是定值1,见解析
的值是定值1,见解析
【解析】
(1)先将抛物线![]() 化为顶点式,由平移规律“上加下减,左加右减”可直接写出抛物线M2的解析式;
化为顶点式,由平移规律“上加下减,左加右减”可直接写出抛物线M2的解析式;
(2)分别求出点A,点B,点C的坐标,求出m的取值范围,再用含m的代数式表示出△CPQ的面积,可用函数的思想求出其最大值;
(3)设直线OB向下平移k个单位长度得到直线EH,分别求出点E,F,G,H的横坐标,分别过G,H作![]() 轴的平行线,过E,F作
轴的平行线,过E,F作![]() 轴的平行线,构造相似三角形△GEM与△HFN,可通过相似三角形的性质求出
轴的平行线,构造相似三角形△GEM与△HFN,可通过相似三角形的性质求出![]() 的值为1.
的值为1.
解:(1)![]() ,
,
![]() 将其先向右平移3个单位,再向上平移3个单位的解析式为:
将其先向右平移3个单位,再向上平移3个单位的解析式为:![]() ;
;
(2)![]() 抛物线
抛物线![]() 与
与![]() 交于点
交于点![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() ,
,
将点![]() 代入
代入![]() ,
,
得:![]() ,
,
![]() ,
,
![]() 抛物线
抛物线![]() 与直线
与直线![]() 交于点
交于点![]() ,
,
![]() ,
,
解得:![]() ,
,![]() ,
,
![]() ,
,
![]() 点
点![]() 的横坐标为
的横坐标为![]() ,
,
![]() 点
点![]() ,
,
则![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
在![]() 中,当
中,当![]() 时,
时,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 在
在![]() 中,
中,
根据二次函数的图象及性质可知,当![]() 时,
时,![]() 有最大值,最大值为6;
有最大值,最大值为6;
(3)![]() 的值是定值1.理由如下:
的值是定值1.理由如下:
设将直线![]() 向下平移
向下平移![]() 个单位长度得到直线
个单位长度得到直线![]() ,
,
则![]() ,
,
![]() 令
令![]() ,
,
解得:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
令![]() ,
,
解得:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
分别过![]() ,
,![]() 作
作![]() 轴的平行线,过
轴的平行线,过![]() ,
,![]() 作
作![]() 轴的平行线,交点分别为
轴的平行线,交点分别为![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() 的值是定值1.
的值是定值1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目